如图1,在 中, , ,点 、 分别在 、 边上, ,连接 、 、 ,点 、 、 分别是 、 、 的中点,连接 、 、 .
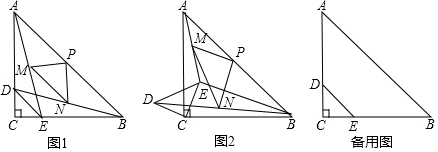
(1) 与 的数量关系是 ;
(2)将 绕点 逆时针旋转到如图2的位置,判断(1)中的结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
(3)若 , ,在将图1中的 绕点 逆时针旋转一周的过程中,当 、 、 三点在一条直线上时, 的长度为 .
相关知识点
推荐套卷
如图1,在 中, , ,点 、 分别在 、 边上, ,连接 、 、 ,点 、 、 分别是 、 、 的中点,连接 、 、 .

(1) 与 的数量关系是 ;
(2)将 绕点 逆时针旋转到如图2的位置,判断(1)中的结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
(3)若 , ,在将图1中的 绕点 逆时针旋转一周的过程中,当 、 、 三点在一条直线上时, 的长度为 .