实验探究:
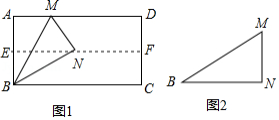
(1)如图1,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 , .请你观察图1,猜想 的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片 剪下,如图2.折叠该纸片,探究 与 的数量关系.写出折叠方案,并结合方案证明你的结论.
如图,在 中, , ,点 、 分别在 、 上,且 ,将 沿 所在直线折叠得到△ (点 在四边形 内),连接 ,则 的长为 .

小颖在学习“两点之间线段最短”查阅资料时发现: 内总存在一点 与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
【特例】如图1,点 为等边 的中心,将 绕点 逆时针旋转 得到 ,从而有 ,连接 得到 ,同时 , ,即 、 、 、 四点共线,故 .在 中,另取一点 ,易知点 与三个顶点连线的夹角不相等,可证明 、 、 、 四点不共线,所以 ,即点 到三个顶点距离之和最小.

【探究】(1)如图2, 为 内一点, ,证明 的值最小;
【拓展】(2)如图3, 中, , , ,且点 为 内一点,求点 到三个顶点的距离之和的最小值.
如图1,在平面直角坐标系, 为坐标原点,点 ,点 .
(1)求 的度数;
(2)如图1,将 绕点 顺时针旋转得△ ,当 恰好落在 边上时,设△ 的面积为 ,△ 的面积为 , 与 有何关系?为什么?
(3)若将 绕点 顺时针旋转到如图2所示的位置, 与 的关系发生变化了吗?证明你的判断.

如图,点 是矩形 的边 上的点, ,将矩形沿着过点 的直线翻折后,点 、 分别落在边 下方的点 、 处,且点 、 、 在同一条直线上,折痕与边 交于点 , 与 交于点 .若 ,那么 的周长为

A. B. C. D.6
已知:如图, 为 的切线, 为切点,过 上一点 作 于点 , 交 于点 , 平分 .
(1)求 的度数;
(2)当 的半径为 ,求 的长.

如图,在等边三角形 中,点 是边 上一定点,点 是直线 上一动点,以 为一边作等边三角形 ,连接 .
【问题解决】
如图1,若点 在边 上,求证: ;
【类比探究】
如图2,若点 在边 的延长线上,请探究线段 , 与 之间存在怎样的数量关系?并说明理由.
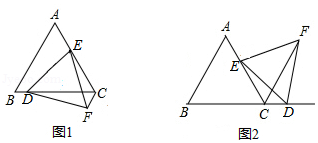
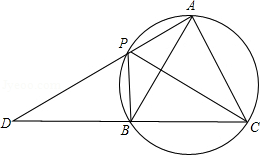
如图, , , , 是圆上的四个点, , , 的延长线相交于点 .
(1)求证: 是等边三角形;
(2)若 , ,求 的长.
如图,在 中,将 沿 折叠后,点 恰好落在 的延长线上的点 处.若 , ,则 的周长为

| A. |
12 |
B. |
15 |
C. |
18 |
D. |
21 |
在 和 中, , .且 ,点 在 的内部,连接 , 和 ,并且 .
(1)如图①,当 时,线段 与 的数量关系为 ,线段 , , 的数量关系为 ;
(2)如图②,当 时,请写出线段 , , 的数量关系,并说明理由;
(3)在(2)的条件下,当点 在线段 上时,若 ,请直接写出 的面积.

如图,在 中, ,点 在线段 上,以 为直径的 与 相交于点 ,与 相交于点 , .
(1)求证: 是 的切线;
(2)若 ,求 的半径 ;
(3)在(1)的条件下,判断以 、 、 、 为顶点的四边形为哪种特殊四边形,并说明理由.
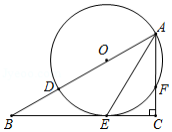
如图,将边长为6的正三角形纸片 按如下顺序进行两次折叠,展平后,得折痕 、 (如图①),点 为其交点.
(1)探求 与 的数量关系,并说明理由;
(2)如图②,若 , 分别为 , 上的动点.
①当 的长度取得最小值时,求 的长度;
②如图③,若点 在线段 上, ,则 的最小值 .
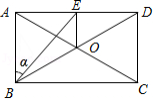
已知:如图,矩形 的对角线 , 相交于点 , , .
(1)求矩形对角线的长;
(2)过 作 于点 ,连结 .记 ,求 的值.