如图,已知 是 的直径,点 为圆上一点,点 为 延长线上一点, , .
(1)求证: 是 的切线.
(2)若 的直径为8,求阴影部分的面积.
如图1, 是半圆 的直径, 是一条弦, 是 上一点, 于点 ,交 于点 ,连结 交 于点 ,且 .
(1)求证:点 平分 ;
(2)如图2所示,延长 至点 ,使 ,连结 .若点 是线段 的中点.求证: 是 的切线.

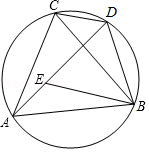
如图,点 是等边三角形 外接圆的 上一点(与点 , 不重合), 交 于点 .
(1)求证: 是等边三角形;
(2)求证: ;
(3)如果 , ,求 的边长.
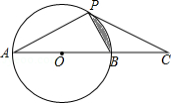
如图,在 中, , ,点 在 边上, 经过点 和点 且与 边相交于点 .
(1)求证: 是 的切线;
(2)若 ,求 的半径.

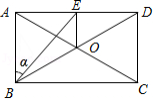
如图,矩形 中, , 相交于点 ,过点 作 交 于点 ,交 于点 ,过点 作 交 于点 ,交 于点 ,连接 , .则下列结论:
① ;
② ;
③ ;
④当 时,四边形 是菱形.
其中,正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在菱形 ABCD中, ,点 E、 F分别在边 AB、 BC上,△ BEF与△ GEF关于直线 EF对称,点 B的对称点是点 G,且点 G在边 AD上.若 , ,则 FG的长为 .

如图,在 中,将 沿 折叠后,点 恰好落在 的延长线上的点 处.若 , ,则 的周长为

| A. |
12 |
B. |
15 |
C. |
18 |
D. |
21 |
定义:有一组对角互余的四边形叫做对余四边形.
理解:
(1)若四边形 是对余四边形,则 与 的度数之和为 ;
证明:
(2)如图1, 是 的直径,点 , , 在 上, , 相交于点 .
求证:四边形 是对余四边形;
探究:
(3)如图2,在对余四边形 中, , ,探究线段 , 和 之间有怎样的数量关系?写出猜想,并说明理由.

如图,在四边形 中, , , ,过点 的 与边 , 分别交于 , 两点. ,垂足为 , .连接 , , .

(1)若 ,试判断 的形状,并说明理由;
(2)若 ,求证: 与 相切于点 .
如图,在一张矩形纸片 ABCD中, AB=3,点 P, Q分别是 AB和 CD的中点,现将这张纸片折叠,使点 D落到 PQ上的点 G处,折痕为 CH,若 HG的延长线恰好经过点 B,则 AD的长为 .
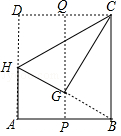
已知:如图,矩形 的对角线 , 相交于点 , , .
(1)求矩形对角线的长;
(2)过 作 于点 ,连结 .记 ,求 的值.