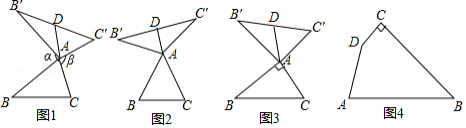
我们定义:如图1,在中,把
绕点
顺时针旋转
得到
,把
绕点
逆时针旋转
得到
,连接
.当
时,我们称△
是
的“旋补三角形”,△
边
上的中线
叫做
的“旋补中线”,点
叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△是
的“旋补三角形”,
是
的“旋补中线”.
①如图2,当为等边三角形时,
与
的数量关系为
;
②如图3,当,
时,则
长为 .
猜想论证:
(2)在图1中,当为任意三角形时,猜想
与
的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形,
,
,
,
,
.在四边形内部是否存在点
,使
是
的“旋补三角形”?若存在,给予证明,并求
的“旋补中线”长;若不存在,说明理由.
如图1,,
分别在射线
,
上,且
为钝角,现以线段
,
为斜边向
的外侧作等腰直角三角形,分别是
,
,点
,
,
分别是
,
,
的中点.
(1)求证:;
(2)延长,
交于点
.
①如图2,若,求证:
为等边三角形;
②如图3,若,求
大小和
的值.

如图1, 是边长为 的等边三角形,边 在射线 上,且 ,点 从 点出发,沿 的方向以 的速度运动,当 不与点 重合时,将 绕点 逆时针方向旋转 得到 ,连接 .
(1)求证: 是等边三角形;
(2)如图2,当 时, 的周长是否存在最小值?若存在,求出 的最小周长;若不存在,请说明理由;
(3)如图3,当点 在射线 上运动时,是否存在以 、 、 为顶点的三角形是直角三角形?若存在,求出此时 的值;若不存在,请说明理由.

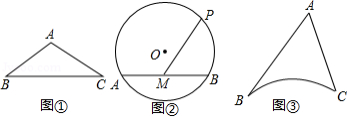
问题提出
(1)如图①,在中,
,
,则
的外接圆半径
的值为 .
问题探究
(2)如图②,的半径为13,弦
,
是
的中点,
是
上一动点,求
的最大值.
问题解决
(3)如图③所示,、
、
是某新区的三条规划路,其中
,
,
,
所对的圆心角为
,新区管委会想在
路边建物资总站点
,在
,
路边分别建物资分站点
、
,也就是,分别在
、线段
和
上选取点
、
、
.由于总站工作人员每天都要将物资在各物资站点间按
的路径进行运输,因此,要在各物资站点之间规划道路
、
和
.为了快捷、环保和节约成本.要使得线段
、
、
之和最短,试求
的最小值.(各物资站点与所在道路之间的距离、路宽均忽略不计)
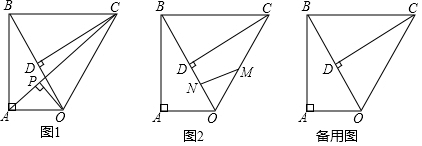
已知Rt△ OAB,∠ OAB=90°,∠ ABO=30°,斜边 OB=4,将Rt△ OAB绕点 O顺时针旋转60°,如图1,连接 BC.
(1)填空:∠ OBC= °;
(2)如图1,连接 AC,作 OP⊥ AC,垂足为 P,求 OP的长度;
(3)如图2,点 M, N同时从点 O出发,在△ OCB边上运动, M沿 O→ C→ B路径匀速运动, N沿 O→ B→ C路径匀速运动,当两点相遇时运动停止,已知点 M的运动速度为1.5单位/秒,点 N的运动速度为1单位/秒,设运动时间为 x秒,△ OMN的面积为 y,求当 x为何值时 y取得最大值?最大值为多少?
发现规律
(1)如图①, 与 都是等边三角形,直线 , 交于点 .直线 , 交于点 .求 的度数.
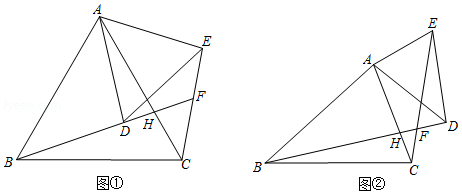
(2)已知: 与 的位置如图②所示,直线 , 交于点 .直线 , 交于点 .若 , ,求 的度数.
应用结论
(3)如图③,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 , 为 轴上一动点,连接 .将线段 绕点 逆时针旋转 得到线段 ,连接 , .求线段 长度的最小值.
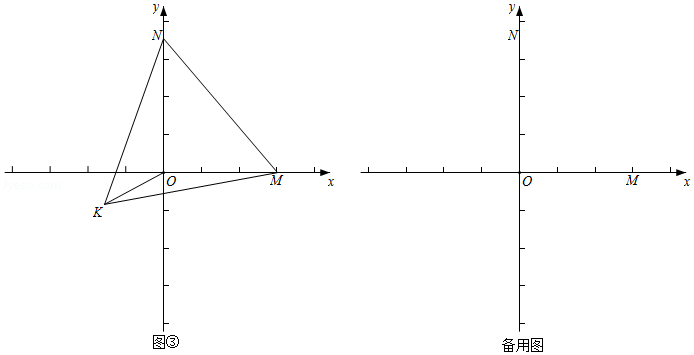
如图1,在平面直角坐标系, 为坐标原点,点 ,点 .
(1)求 的度数;
(2)如图1,将 绕点 顺时针旋转得△ ,当 恰好落在 边上时,设△ 的面积为 ,△ 的面积为 , 与 有何关系?为什么?
(3)若将 绕点 顺时针旋转到如图2所示的位置, 与 的关系发生变化了吗?证明你的判断.

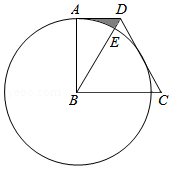
如图,四边形 内接于圆, ,对角线 平分 .
(1)求证: 是等边三角形;
(2)过点 作 交 的延长线于点 ,若 , ,求 的面积.

如图,四边形 中, , , ,连接 ,以点 为圆心, 长为半径作 ,交 于点 .
(1)试判断 与 的位置关系,并说明理由;
(2)若 , ,求图中阴影部分的面积.
已知在 中, , 是 边上的一点,将 沿着过点 的直线折叠,使点 落在 边的点 处(不与点 , 重合),折痕交 边于点 .
(1)特例感知 如图1,若 , 是 的中点,求证: ;
(2)变式求异 如图2,若 , , ,过点 作 于点 ,求 和 的长;
(3)化归探究 如图3,若 , ,且当 时,存在两次不同的折叠,使点 落在 边上两个不同的位置,请直接写出 的取值范围.

如图1, 是半圆 的直径, 是一条弦, 是 上一点, 于点 ,交 于点 ,连结 交 于点 ,且 .
(1)求证:点 平分 ;
(2)如图2所示,延长 至点 ,使 ,连结 .若点 是线段 的中点.求证: 是 的切线.

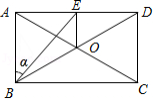
已知:如图,矩形 的对角线 , 相交于点 , , .
(1)求矩形对角线的长;
(2)过 作 于点 ,连结 .记 ,求 的值.
如图,四边形 为矩形, 是对角线 的中点.连接 并延长至 ,使 ,以 , 为邻边作菱形 ,连接 .
(1)判断四边形 的形状,并证明你的结论.
(2)连接 ,若 ,求 的长.

问题背景:如图1,等腰 中, , ,作 于点 ,则 为 的中点, ,于是 ;
迁移应用:如图2, 和 都是等腰三角形, , , , 三点在同一条直线上,连接 .
①求证: ;
②请直接写出线段 , , 之间的等量关系式;
拓展延伸:如图3,在菱形 中, ,在 内作射线 ,作点 关于 的对称点 ,连接 并延长交 于点 ,连接 , .
①证明 是等边三角形;
②若 , ,求 的长.
