如图,在矩形 中,对角线 的垂直平分线 分别交 、 、 于点 、 、 ,连接 和 .
(1)求证:四边形 为菱形;
(2)若 , ,求菱形 的周长.

如图,在 中, , , , 、 分别是斜边 、直角边 上的点,把 沿着直线 折叠.

(1)如图1,当折叠后点 和点 重合时,用直尺和圆规作出直线 ;(不写作法和证明,保留作图痕迹)
(2)如图2,当折叠后点 落在 边上点 处,且四边形 是菱形时,求折痕 的长.
如图,在 中, ,
(1)尺规作图(保留作图痕迹,不写作法)
①作 的垂直平分线,垂足为 ;
②以 为圆心, 长为半径作圆,交 于 异于 ,连接 ;
(2)探究 与 的位置关系,并证明你的结论.

平行四边形 中, , , 的中垂线分别交 , 于点 , ,垂足为 .
(1)求证: ;
(2)若 ,求 的值.

如图, 中, 是 上一点, 于点 , 是 的中点, 于点 ,与 交于点 ,若 , 平分 ,连接 , .
(1)求证: ;
(2)小亮同学经过探究发现: .请你帮助小亮同学证明这一结论.
(3)若 ,判定四边形 是否为菱形,并说明理由.

问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于 ,那么它所对的直角边等于斜边的一半.即:如图1,在 中, , ,则: .
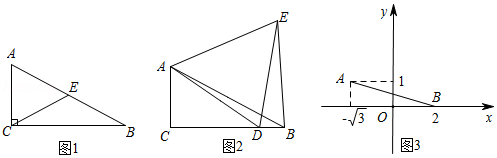
探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接 边上中线 ,由于 ,易得结论:① 为等边三角形;② 与 之间的数量关系为 .
(2)如图2,点 是边 上任意一点,连接 ,作等边 ,且点 在 的内部,连接 .试探究线段 与 之间的数量关系,写出你的猜想并加以证明.
(3)当点 为边 延长线上任意一点时,在(2)条件的基础上,线段 与 之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系 中,点 的坐标为 , ,点 是 轴正半轴上的一动点,以 为边作等边 ,当 点在第一象限内,且 时,求 点的坐标.
已知:如图, ,射线 上一点 .
求作:等腰 ,使线段 为等腰 的底边,点 在 内部,且点 到 两边的距离相等.
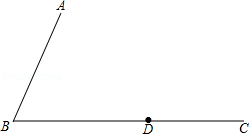
如图, 的对角线 、 相交于点 , 过点 且与 、 分别相交于点 、 ,连接 .
(1)求证: ;
(2)若 , 的周长是10,求 的周长.

如图,在 中, , ,动点 从点 出发以 的速度沿 匀速运动,同时动点 从点 出发以 的速度沿 匀速运动,当点 到达点 时,点 、 同时停止运动,设运动时间为 .
(1)当 为何值时,点 在线段 的垂直平分线上?
(2)是否存在某一时刻 ,使 是以 为腰的等腰三角形?若存在,求出 的值;若不存在,请说明理由;
(3)以 为边,往 方向作正方形 ,设四边形 的面积为 ,求 关于 的函数关系式.

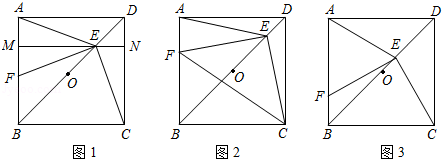
已知点 是正方形 对角线 的中点.
(1)如图1,若点 是 的中点,点 是 上一点,且使得 ,过点 作 ,交 于点 ,交 于点 .求证:
① ; ②点 是 的中点;
(2)如图2,若点 是 上一点,点 是 上一点,且使 ,请判断 的形状,并说明理由;
(3)如图3,若 是 上的动点(不与 , 重合),连接 ,过 点作 ,交 于点 ,当 时,请猜想 的值(请直接写出结论).
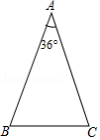
如图,已知等腰 顶角 .
(1)在 上作一点 ,使 (要求:尺规作图,保留作图痕迹,不必写作法和证明,最后用黑色墨水笔加黑);
(2)求证: 是等腰三角形.
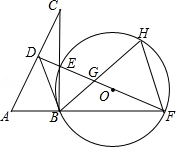
如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点 , , , 是 的外接圆, 的平分线交 于点 ,交 于点 ,连接 、 .
(1)试判断 与 的位置关系,并说明理由;
(2)当 时,求 的面积;
(3)在(2)的条件下,求 的值.
如图,在Rt△ABC中, .
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹:
①作∠ACB的平分线,交斜边AB于点D;
②过点D作AC的垂线,垂足为点E.
(2)在(1)作出的图形中,若 , ,则DE= .

在数学课本上,同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程:
已知:直线l和l外一点P.

求作:直线l的垂线,使它经过点P.
作法:如图:(1)在直线l上任取两点A、B;
(2)分别以点A、B为圆心,AP,BP长为半径画弧,两弧相交于点Q;
(3)作直线PQ.
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是:
(2)已知,直线l和l外一点P,
求作:⊙P,使它与直线l相切.(尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
