初中数学线段垂直平分线的性质解答题

如图，在中，，，．

（1）尺规作图：不写作法，保留作图痕迹．

①作的平分线，交斜边于点；

②过点作的垂线，垂足为点．

（2）在（1）作出的图形中，求的长．

如图，在中，．

（1）已知线段的垂直平分线与边交于点，连接，求证：．

（2）以点为圆心，线段的长为半径画弧，与边交于点，连接．若，求的度数．

在中，平分交于点．

（1）如图1，若，，求的面积；

（2）如图2，过点作，交的延长线于点，分别交，于点，，且．求证：．

在 $\mathit{\Delta ABC}$ 中， $\angle B=45°$ ， $\angle C=30°$ ，点 $D$ 是 $\mathit{BC}$ 上一点，连接 $\mathit{AD}$ ，过点 $A$ 作 $\mathit{AG}\perp \mathit{AD}$ ，在 $\mathit{AG}$ 上取点 $F$ ，连接 $\mathit{DF}$ ．延长 $\mathit{DA}$ 至 $E$ ，使 $\mathit{AE}=\mathit{AF}$ ，连接 $\mathit{EG}$ ， $\mathit{DG}$ ，且 $\mathit{GE}=\mathit{DF}$ ．

（1）若 $\mathit{AB}=2\sqrt{2}$ ，求 $\mathit{BC}$ 的长；

（2）如图1，当点 $G$ 在 $\mathit{AC}$ 上时，求证： $\mathit{BD}=\frac{1}{2}\mathit{CG}$ ；

（3）如图2，当点 $G$ 在 $\mathit{AC}$ 的垂直平分线上时，直接写出 $\frac{\mathit{AB}}{\mathit{CG}}$ 的值．

已知：如图，、是的两条弦，且，是延长线上一点，联结并延长交于点，联结并延长交于点．

（1）求证：；

（2）如果，求证：四边形是菱形．

如图，已知中，，．

（1）求边的长；

（2）设边的垂直平分线与边的交点为，求的值．

已知在平面直角坐标系中（如图），已知抛物线经过点，对称轴是直线，顶点为．

（1）求这条抛物线的表达式和点的坐标；

（2）点在对称轴上，且位于顶点上方，设它的纵坐标为，联结，用含的代数式表示的余切值；

（3）将该抛物线向上或向下平移，使得新抛物线的顶点在轴上．原抛物线上一点平移后的对应点为点，如果，求点的坐标．

问题发现

（1）如图（1），四边形 $\mathit{ABCD}$ 中，若 $\mathit{AB}=\mathit{AD}$ ， $\mathit{CB}=\mathit{CD}$ ，则线段 $\mathit{BD}$ ， $\mathit{AC}$ 的位置关系为 　 　；

拓展探究

（2）如图（2），在 $\text{Rt}\Delta \text{ABC}$ 中，点 $F$ 为斜边 $\mathit{BC}$ 的中点，分别以 $\mathit{AB}$ ， $\mathit{AC}$ 为底边，在 $\text{Rt}\Delta \text{ABC}$ 外部作等腰三角形 $\mathit{ABD}$ 和等腰三角形 $\mathit{ACE}$ ，连接 $\mathit{FD}$ ， $\mathit{FE}$ ，分别交 $\mathit{AB}$ ， $\mathit{AC}$ 于点 $M$ ， $N$ ，试猜想四边形 $\mathit{FMAN}$ 的形状，并说明理由；

解决问题

（3）如图（3），在正方形 $\mathit{ABCD}$ 中， $\mathit{AB}=2\sqrt{2}$ ，以点 $A$ 为旋转中心将正方形 $\mathit{ABCD}$ 旋转 $60°$ ，得到正方形 $\mathit{AB}\text{'}C\text{'}D\text{'}$ ，请直接写出 $\mathit{BD}\text{'}$ 的长度．

如图，已知的中垂线交于点，交于点，有下面3个结论：

①是等腰三角形；
②∽；
③点D是线段AC的黄金分割点．
请你从以上结论中只选一个加以证明

如图，已知D是BC的中点，过点D作BC的垂线交∠A的平分线于点E，EF⊥AB于点F，EG⊥AC于点G．求证：BF=CG．

如图，已知△ABC，用直尺（没有刻度）和圆规在平面上求作一个点P，使P到∠A两边的距离相等，且PA=PB．（不要求写作法，但要保留作图痕迹）

画图、证明：如图，∠AOB=90°，点C、D分别在OA、OB上．

（1）尺规作图（不写作法，保留作图痕迹）：
作∠AOB的平分线OP；作线段CD的垂直平分线EF，分别与CD、OP相交于E、F；连接OE、CF、DF．
（2）在所画图中，线段OE与CD之间有怎样的数量关系，线段DF与CF之间有怎样的数量关系，并说明理由．

如图，点D在BC上，DE垂直平分AC，垂足为E，F是BA的中点．

求证：DF是AB的垂直平分线．

如图所示，要在公园（四边形ABCD）中建造一座音乐喷泉，喷泉位置应符合如下要求：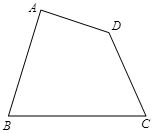

（1）到公园两个出入口A、C的距离相等；
（2）到公园两边围墙AB、AD的距离相等．
请你用尺规作图的方法确定喷泉的位置P．（不必写作法，但要保留作图痕迹）

作图题：某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵黄桷树．如图，要求黄桷树的位置点P到边AB、BC的距离相等，并且点P到点A、D的距离也相等．请用尺规作图作出栽种黄桷树的位置点P（不写作法，保留作图痕迹）．