问题发现
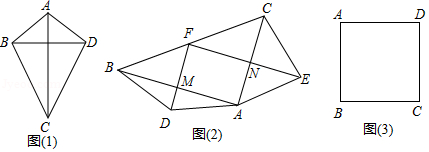
(1)如图(1),四边形 中,若 , ,则线段 , 的位置关系为 ;
拓展探究
(2)如图(2),在 中,点 为斜边 的中点,分别以 , 为底边,在 外部作等腰三角形 和等腰三角形 ,连接 , ,分别交 , 于点 , ,试猜想四边形 的形状,并说明理由;
解决问题
(3)如图(3),在正方形 中, ,以点 为旋转中心将正方形 旋转 ,得到正方形 ,请直接写出 的长度.
相关知识点
推荐套卷
问题发现
(1)如图(1),四边形 中,若 , ,则线段 , 的位置关系为 ;
拓展探究
(2)如图(2),在 中,点 为斜边 的中点,分别以 , 为底边,在 外部作等腰三角形 和等腰三角形 ,连接 , ,分别交 , 于点 , ,试猜想四边形 的形状,并说明理由;
解决问题
(3)如图(3),在正方形 中, ,以点 为旋转中心将正方形 旋转 ,得到正方形 ,请直接写出 的长度.
