江苏省常州市八年级上学期期中考试数学试卷
下列条件中,不能判断△ABC为直角三角形的是( )
| A.a2=1 ,b2=2 ,c2=3 |
| B.a∶b∶c=3∶4∶5 |
| C.∠A+∠B=∠C |
| D.∠A∶∠B∶∠C=3∶4∶5 |
如图,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E.BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )

| A.1组 | B.2组 | C.3组 | D.4组 |
如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
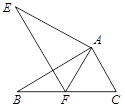
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合,若BC=5,CD=3,则BD的长为( )

| A.1 | B.2 | C.3 | D.4 |
如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )

| A.4.5cm | B.5.5cm | C.6.5cm | D.7cm |
如图,△ABC是等边三角形,P是BC上任意一点,PD⊥AB于D,PE⊥AC于E,连接DE.记△ADE的周长为L1,四边形BDEC的周长为L2,则L1与L2的大小关系是 ( )

| A.Ll=L2 | B.L1>L2 | C.L2>L1 | D.无法确定 |
△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为 ( )
| A.7 | B.7或11 | C.11 | D.7或10 |
如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于 .

如图,△ABC中,AB=AC,边AC的垂直平分线分别交边AB、AC于点E、F.如果∠B=75°,那么∠BCE= 度.

如图,△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为 .
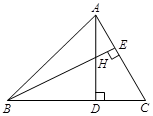
如图,△ABC中,∠BAC=110°,E、G分别为AB、AC中点,DE⊥AB,FG⊥AC,则∠DAF= °.

如图,△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为 .

如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿着直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为 cm.

如图,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为 .
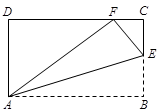
如图所示,要在公园(四边形ABCD)中建造一座音乐喷泉,喷泉位置应符合如下要求:
(1)到公园两个出入口A、C的距离相等;
(2)到公园两边围墙AB、AD的距离相等.
请你用尺规作图的方法确定喷泉的位置P.(不必写作法,但要保留作图痕迹)
在△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15,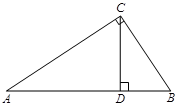
(1)求AB的长;
(2)求CD的长.
如图,在△ABC中,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF.
求证:(1)△BDE≌△CDF;
(2)AB=AC.
一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,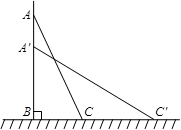
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到A′,那么梯子的底端在水平方向滑动了几米?
如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.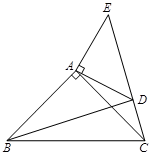
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.








 粤公网安备 44130202000953号
粤公网安备 44130202000953号