如图, 中, 是 上一点, 于点 , 是 的中点, 于点 ,与 交于点 ,若 , 平分 ,连接 , .
(1)求证: ;
(2)小亮同学经过探究发现: .请你帮助小亮同学证明这一结论.
(3)若 ,判定四边形 是否为菱形,并说明理由.
推荐套卷
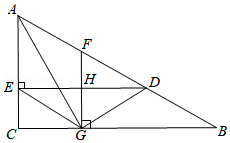
如图, 中, 是 上一点, 于点 , 是 的中点, 于点 ,与 交于点 ,若 , 平分 ,连接 , .
(1)求证: ;
(2)小亮同学经过探究发现: .请你帮助小亮同学证明这一结论.
(3)若 ,判定四边形 是否为菱形,并说明理由.
