如图1和图2,在中,
,
,
.点
在
边上,点
,
分别在
,
上,且
.点
从点
出发沿折线
匀速移动,到达点
时停止;而点
在
边上随
移动,且始终保持
.
(1)当点在
上时,求点
与点
的最短距离;
(2)若点在
上,且
将
的面积分成上下
两部分时,求
的长;
(3)设点移动的路程为
,当
及
时,分别求点
到直线
的距离(用含
的式子表示);
(4)在点处设计并安装一扫描器,按定角
扫描
区域(含边界),扫描器随点
从
到
再到
共用时36秒.若
,请直接写出点
被扫描到的总时长.

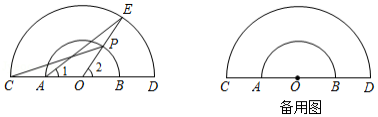
如图,点为
中点,分别延长
到点
,
到点
,使
.以点
为圆心,分别以
,
为半径在
上方作两个半圆.点
为小半圆上任一点(不与点
,
重合),连接
并延长交大半圆于点
,连接
,
.
(1)①求证:;
②写出,
和
三者间的数量关系,并说明理由.
(2)若,当
最大时,直接指出
与小半圆的位置关系,并求此时
(答案保留
.
如图,和
中,
,
,
,边
与边
交于点
(不与点
,
重合),点
,
在
异侧,
为
的内心.
(1)求证:;
(2)设,请用含
的式子表示
,并求
的最大值;
(3)当时,
的取值范围为
,分别直接写出
,
的值.

已知:整式,整式
.
尝试 化简整式.
发现,求整式
.
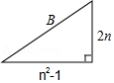
联想 由上可知,,当
时,
,
,
为直角三角形的三边长,如图.填写下表中
的值:
直角三角形三边 |
|||
勾股数组Ⅰ |
8 |
17 |
|
勾股数组Ⅱ |
35 |
|
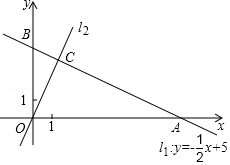
如图,直角坐标系中,一次函数
的图象
分别与
,
轴交于
,
两点,正比例函数的图象
与
交于点
.
(1)求的值及
的解析式;
(2)求的值;
(3)一次函数的图象为
,且
,
,
不能围成三角形,直接写出
的值.
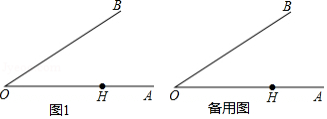
如图,,
为
中点,点
为射线
上(不与点
重合)的任意一点,连接
,并使
的延长线交射线
于点
,设
.
(1)求证:;
(2)当时,求
的度数;
(3)若的外心在该三角形的内部,直接写出
的取值范围.

平面内,如图,在中,
,
,
,点
为
边上任意点,连接
,将
绕点
逆时针旋转
得到线段
.
(1)当时,求
的大小;
(2)当时,求点
与点
间的距离(结果保留根号);
(3)若点恰好落在
的边所在的直线上,直接写出
旋转到
所扫过的面积.(结果保留

如图,,
为
中点,点
在线段
上(不与点
,
重合),将
绕点
逆时针旋转
后得到扇形
,
,
分别切优弧
于点
,
,且点
,
在
异侧,连接
.
(1)求证:;
(2)当时,求
的长(结果保留
;
(3)若的外心在扇形
的内部,求
的取值范围.

如图,中,
,
,
为
内部一点,且
.
(1)求证:;
(2)求证:;
(3)若点到三角形的边
,
,
的距离分别为
,
,
,求证
.

已知,
为射线
上一定点,
,
为射线
上一点,
为线段
上一动点,连接
,满足
为钝角,以点
为中心,将线段
顺时针旋转
,得到线段
,连接
.
(1)依题意补全图1;
(2)求证:;
(3)点关于点
的对称点为
,连接
.写出一个
的值,使得对于任意的点
总有
,并证明.
如图,在正方形中,
是边
上的一动点(不与点
、
重合),连接
,点
关于直线
的对称点为
,连接
并延长交
于点
,连接
,过点
作
交
的延长线于点
,连接
.
(1)求证:;
(2)用等式表示线段与
的数量关系,并证明.

如图,是
的直径,过
外一点
作
的两条切线
,
,切点分别为
,
,连接
,
.
(1)求证:;
(2)连接,
,若
,
,
,求
的长.

如图,在四边形中,
,
,对角线
,
交于点
,
平分
,过点
作
交
的延长线于点
,连接
.
(1)求证:四边形是菱形;
(2)若,
,求
的长.
