如图①,在中,
,过
上一点
作
交
于点
,以
为顶点,
为一边,作
,另一边
交
于点
.
(1)求证:四边形为平行四边形;
(2)当点为
中点时,
的形状为 ;
(3)延长图①中的到点
,使
,连接
,
,
,得到图②,若
,判断四边形
的形状,并说明理由.

如图,在中,
,
,
,动点
从点
出发,沿
以每秒2个单位长度的速度向终点
运动.过点
作
于点
(点
不与点
、
重合),作
,边
交射线
于点
.设点
的运动时间为
秒.
(1)用含的代数式表示线段
的长;
(2)当点与点
重合时,求
的值;
(3)设与
重叠部分图形的面积为
,求
与
之间的函数关系式;
(4)当线段的垂直平分线经过
一边中点时,直接写出
的值.

在正方形中,
是边
上一点(点
不与点
、
重合),连结
.

【感知】如图①,过点作
交
于点
.易证
.(不需要证明)
【探究】如图②,取的中点
,过点
作
交
于点
,交
于点
.
(1)求证:.
(2)连结,若
,则
的长为 .
【应用】如图③,取的中点
,连结
.过点
作
交
于点
,连结
、
.若
,则四边形
的面积为 .
图①、图②均是的正方形网格,每个小正方形的顶点称为格点,线段
、
的端点均在格点上.在图①、图②给定的网格中以
、
为邻边各画一个四边形,使第四个顶点在格点上.要求:

(1)所画的两个四边形均是轴对称图形.
(2)所画的两个四边形不全等.
如图,在中,
,
,
.点
从点
出发,以
的速度沿边
向终点
运动.过点
作
交折线
于点
,
为
中点,以
为边向右侧作正方形
.设正方形
与
重叠部分图形的面积是
,点
的运动时间为
.

(1)当点在边
上时,正方形
的边长为
(用含
的代数式表示);
(2)当点不与点
重合时,求点
落在边
上时
的值;
(3)当时,求
关于
的函数解析式;
(4)直接写出边的中点落在正方形
内部时
的取值范围.
如图,在平面直角坐标系中,直线与函数
的图象交于点
,
.过点
作
平行于
轴交
轴于点
,在
轴负半轴上取一点
,使
,且
的面积是6,连接
.
(1)求,
,
的值;
(2)求的面积.

图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段的端点在格点上.

(1)在图①、图2中,以为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全等)
(2)在图③中,以为边画一个平行四边形,且另外两个顶点在格点上.
如图①,在中,
,
,
,点
从点
出发,沿折线
向终点
运动,在
上以每秒5个单位长度的速度运动,在
上以每秒3个单位长度的速度运动,点
从点
出发,沿
方向以每秒
个单位长度的速度运动,
,
两点同时出发,当点
停止时,点
也随之停止.设点
运动的时间为
秒.
(1)求线段的长;(用含
的代数式表示)
(2)连结,当
与
的一边平行时,求
的值;
(3)如图②,过点作
于点
,以
,
为邻边作矩形
,点
为
的中点,连结
.设矩形
与
重叠部分图形的面积为
.①当点
在线段
上运动时,求
与
之间的函数关系式;②直接写出
将矩形
分成两部分的面积比为
时
的值.

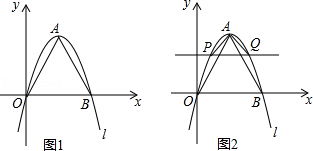
如图1,在平面直角坐标系中,点在
轴正半轴上,
的长度为
,以
为边向上作等边三角形
,抛物线
经过点
,
,
三点
(1)当时,
,当
时,
;
(2)根据(1)中的结果,猜想与
的关系,并证明你的结论;
(3)如图2,在图1的基础上,作轴的平行线交抛物线
于
、
两点,
的长度为
,当
为等腰直角三角形时,
和
的关系式为 ;
(4)利用(2)(3)中的结论,求与
的面积比.
如图,在等腰直角三角形中,
,
,
于点
,点
从点
出发,沿
方向以
的速度运动到点
停止,在运动过程中,过点
作
交
于点
,以线段
为边作等腰直角三角形
,且
(点
,
位于
异侧).设点
的运动时间为
,
与
重叠部分的面积为
(1)当点落在
上时,
;
(2)当点落在
上时,
;
(3)求关于
的函数解析式,并写出自变量
的取值范围.

(1)如图1,在中,
,以点
为中心,把
逆时针旋转
,得到△
;再以点
为中心,把
顺时针旋转
,得到△
,连接
,则
与
的位置关系为 ;
(2)如图2,当是锐角三角形,
时,将
按照(1)中的方式旋转
,连接
,探究
与
的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接,若
,△
的面积为4,则△
的面积为 .
