如图,在中,,,.点从点出发,以的速度沿边向终点运动.过点作交折线于点,为中点,以为边向右侧作正方形.设正方形与重叠部分图形的面积是,点的运动时间为.
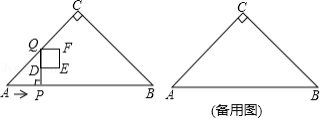
(1)当点在边上时,正方形的边长为 (用含的代数式表示);
(2)当点不与点重合时,求点落在边上时的值;
(3)当时,求关于的函数解析式;
(4)直接写出边的中点落在正方形内部时的取值范围.
推荐套卷
如图,在中,,,.点从点出发,以的速度沿边向终点运动.过点作交折线于点,为中点,以为边向右侧作正方形.设正方形与重叠部分图形的面积是,点的运动时间为.

(1)当点在边上时,正方形的边长为 (用含的代数式表示);
(2)当点不与点重合时,求点落在边上时的值;
(3)当时,求关于的函数解析式;
(4)直接写出边的中点落在正方形内部时的取值范围.