（宜宾）如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（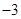
，
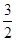），AB=1，AD=2．
（1）直接写出B、C、D三点的坐标；
（2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数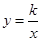
（
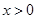）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．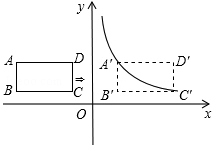
相关试题
（宜宾）如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A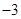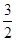（，），AB=1，AD=2．
（1）直接写出B、C、D三点的坐标；
（2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数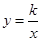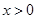（）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．
； 
粤公网安备 44130202000953号