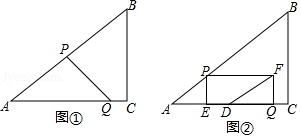如图①,在中,,,,点从点出发,沿折线向终点运动,在上以每秒5个单位长度的速度运动,在上以每秒3个单位长度的速度运动,点从点出发,沿方向以每秒个单位长度的速度运动,,两点同时出发,当点停止时,点也随之停止.设点运动的时间为秒.
(1)求线段的长;(用含的代数式表示)
(2)连结,当与的一边平行时,求的值;
(3)如图②,过点作于点,以,为邻边作矩形,点为的中点,连结.设矩形与重叠部分图形的面积为.①当点在线段上运动时,求与之间的函数关系式;②直接写出将矩形分成两部分的面积比为时的值.
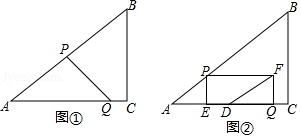
推荐套卷
如图①,在中,,,,点从点出发,沿折线向终点运动,在上以每秒5个单位长度的速度运动,在上以每秒3个单位长度的速度运动,点从点出发,沿方向以每秒个单位长度的速度运动,,两点同时出发,当点停止时,点也随之停止.设点运动的时间为秒.
(1)求线段的长;(用含的代数式表示)
(2)连结,当与的一边平行时,求的值;
(3)如图②,过点作于点,以,为邻边作矩形,点为的中点,连结.设矩形与重叠部分图形的面积为.①当点在线段上运动时,求与之间的函数关系式;②直接写出将矩形分成两部分的面积比为时的值.