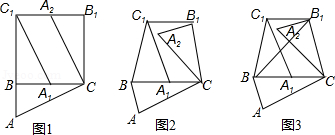
(1)如图1,在中,,以点为中心,把逆时针旋转,得到△;再以点为中心,把顺时针旋转,得到△,连接,则与的位置关系为 ;
(2)如图2,当是锐角三角形,时,将按照(1)中的方式旋转,连接,探究与的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接,若,△的面积为4,则△的面积为 .
推荐套卷
(1)如图1,在中,,以点为中心,把逆时针旋转,得到△;再以点为中心,把顺时针旋转,得到△,连接,则与的位置关系为 ;
(2)如图2,当是锐角三角形,时,将按照(1)中的方式旋转,连接,探究与的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接,若,△的面积为4,则△的面积为 .
