如图,已知四边形ABCD中,∠C=∠D=90°,AE平分∠DAB,BE平分∠ABC,且E在D上.
(1)求∠AEB;
(2)求证:DE=CE.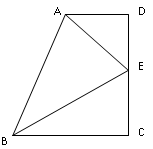
已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判定△ABC的形状.
如图,已知 的中垂线
的中垂线 交
交 于点
于点 ,交
,交 于点
于点 ,有下面3个结论:
,有下面3个结论:
① 是等腰三角形;
是等腰三角形;
② ∽
∽ ;
;
③点D是线段AC的黄金分割点.
请你从以上结论中只选一个加以证明
如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D已知经过点D的⊙O切线恰好经过点C

(1)试判断CD与AC的位置关系,并证明;
(2)若△ACB∽△CDB,且AC=3,求图中阴影部分的面积
如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q.记△AEF的面积为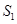 ,四边形EFQP的面积为
,四边形EFQP的面积为 ,四边形PQCB的面积为
,四边形PQCB的面积为
(1)求证:EF+PQ=BC
(2)若 +
+ =
= ,求
,求 的值
的值
(3)若 -
-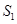 =
= ,直接写出
,直接写出 的值
的值
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)当t为何值时,△CPQ为等腰三角形?
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
中国对南沙群岛及其附近海域拥有无可争辩的主权。2015年10月27日,美国拉森号军舰未经中国政府允许,非法进入中国南沙群岛有关岛礁邻近海域。中国海军盐城舰加大南沙海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,渚碧礁位于 点,盐城舰在点B处发现美国拉森号军舰,自A点出发沿着AO方向匀速驶向渚碧礁所在地
点,盐城舰在点B处发现美国拉森号军舰,自A点出发沿着AO方向匀速驶向渚碧礁所在地 点,盐城舰立即从B处出发以相同的速度沿某直线去拦截拉森号军舰,结果在点C处截住了拉森号军舰.
点,盐城舰立即从B处出发以相同的速度沿某直线去拦截拉森号军舰,结果在点C处截住了拉森号军舰.
(1)请用直尺和圆规作出C处的位置;
(2)求盐城舰行驶的航程BC的长.
阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1) 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.

 求
求 的值;
的值;
 若CD=2,求BP的长.
若CD=2,求BP的长.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线相交于点E,∠ADC=60°.
(1)求证:△ADE是等腰三角形;
(2)若AD=2 ,求BE的长.
,求BE的长.
如图1,在 ,将一块与
,将一块与 全等的三角板的直角顶点放在点C上,一直角边与BC重叠。
全等的三角板的直角顶点放在点C上,一直角边与BC重叠。
(1)操作1:固定 ,将三角板沿
,将三角板沿 方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿
方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿 方向平移的距离为___________;
方向平移的距离为___________;
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度 ,如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
,如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
请阅读下列材料:若 是关于
是关于 的一元二次方程的两个根,则方程的两个根
的一元二次方程的两个根,则方程的两个根 和系数
和系数 有如下关系:
有如下关系: . 我们把它们称为根与系数关系定理.
. 我们把它们称为根与系数关系定理.
如果设二次函数 的图象与x轴的两个交点
的图象与x轴的两个交点 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
请你参考以上定理和结论,解答下列问题:
设二次函数 的图象与x轴的两个交点为
的图象与x轴的两个交点为 ,抛物线的顶点为
,抛物线的顶点为 ,显然
,显然 为等腰三角形。
为等腰三角形。
(1)当 为等腰直角三角形时,求
为等腰直角三角形时,求 的值,
的值,
(2)当 为等边三角形时,求
为等边三角形时,求 的值,
的值,
(3)设抛物线 与
与 轴的两个交点为
轴的两个交点为 、
、 ,顶点为
,顶点为 ,且
,且 ,试问如何平移此抛物线,才能使
,试问如何平移此抛物线,才能使 ?
?