请阅读下列材料:若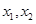 是关于
是关于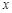 的一元二次方程的两个根,则方程的两个根
的一元二次方程的两个根,则方程的两个根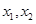 和系数
和系数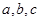 有如下关系:
有如下关系: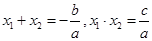 . 我们把它们称为根与系数关系定理.
. 我们把它们称为根与系数关系定理.
如果设二次函数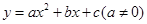 的图象与x轴的两个交点
的图象与x轴的两个交点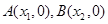 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为: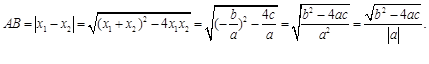
请你参考以上定理和结论,解答下列问题:
设二次函数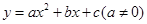 的图象与x轴的两个交点为
的图象与x轴的两个交点为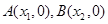 ,抛物线的顶点为
,抛物线的顶点为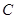 ,显然
,显然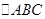 为等腰三角形。
为等腰三角形。
(1)当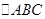 为等腰直角三角形时,求
为等腰直角三角形时,求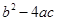 的值,
的值,
(2)当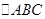 为等边三角形时,求
为等边三角形时,求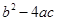 的值,
的值,
(3)设抛物线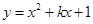 与
与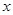 轴的两个交点为
轴的两个交点为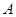 、
、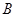 ,顶点为
,顶点为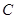 ,且
,且 ,试问如何平移此抛物线,才能使
,试问如何平移此抛物线,才能使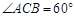 ?
?
推荐套卷
 .
.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号