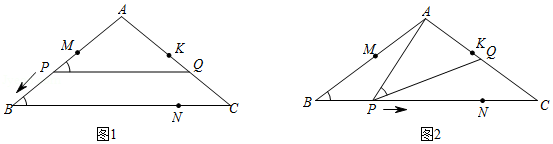
如图1和图2,在中,,,.点在边上,点,分别在,上,且.点从点出发沿折线匀速移动,到达点时停止;而点在边上随移动,且始终保持.
(1)当点在上时,求点与点的最短距离;
(2)若点在上,且将的面积分成上下两部分时,求的长;
(3)设点移动的路程为,当及时,分别求点到直线的距离(用含的式子表示);
(4)在点处设计并安装一扫描器,按定角扫描区域(含边界),扫描器随点从到再到共用时36秒.若,请直接写出点被扫描到的总时长.
相关知识点
推荐套卷
如图1和图2,在中,,,.点在边上,点,分别在,上,且.点从点出发沿折线匀速移动,到达点时停止;而点在边上随移动,且始终保持.
(1)当点在上时,求点与点的最短距离;
(2)若点在上,且将的面积分成上下两部分时,求的长;
(3)设点移动的路程为,当及时,分别求点到直线的距离(用含的式子表示);
(4)在点处设计并安装一扫描器,按定角扫描区域(含边界),扫描器随点从到再到共用时36秒.若,请直接写出点被扫描到的总时长.
