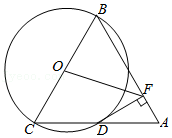
如图,在 中, , , (圆心 在 内部)经过 、 两点,交 于点 ,过点 作 的切线交 于点 .延长 交 于点 ,作 交 于点
(1)求证:四边形 是平行四边形;
(2)若 , ,求 的值.
如图, 是 的角平分线,在 上取点 ,使 .
(1)求证: ;
(2)若 , ,求 的度数.

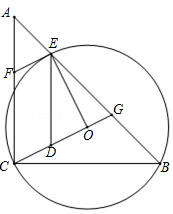
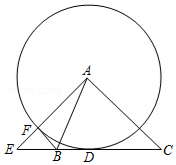
如图,已知等腰直角三角形 ,点 是斜边 上一点(不与 , 重合), 是 的外接圆 的直径.
(1)求证: 是等腰直角三角形;
(2)若 的直径为2,求 的值.

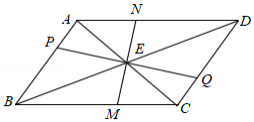
如图,过 对角线 与 的交点 作两条互相垂直的直线,分别交边 、 、 、 于点 、 、 、 .
(1)求证: ;
(2)顺次连接点 、 、 、 ,求证:四边形 是菱形.
在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:

如图,将矩形 的四边 、 、 、 分别延长至 、 、 、 ,使得 , ,连接 , , , .
(1)求证:四边形 为平行四边形;
(2)若矩形 是边长为1的正方形,且 , ,求 的长.
如图, 、 、 分别是 各边的中点,连接 、 、 .
(1)求证:四边形 为平行四边形;
(2)加上条件 后,能使得四边形 为菱形,请从① ;② 平分 ;③ 这三个条件中选择1个条件填空(写序号),并加以证明.

如图,已知: 是 的直径,点 在 上, 是 的切线, 于点 , 是 延长线上一点, 交 于点 ,连接 、 .
(1)求证: 平分 .
(2)若 ,
①求 的度数;
②若 的半径为 ,求线段 的长.
如图,在 和 中, , ,点 , , 依次在同一直线上,且 .
(1)求证: .
(2)连结 ,当 , 时,求 的长.

如图,四边形 为平行四边形,连接 ,且 .请用尺规完成基本作图:作出 的角平分线与 交于点 .连接 交 于点 ,交 于点 ,猜想线段 和线段 的数量关系,并证明你的猜想.(尺规作图保留作图痕迹,不写作法)

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

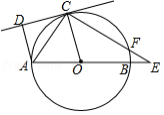
如图,以等边三角形 的 边为直径画圆,交 于点 , 于点 ,连接 ,且 .
(1)求证: 是 的切线;
(2)求线段 的长度.