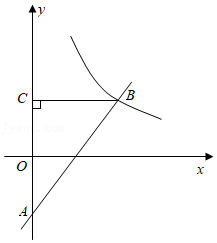
如图,在 中, , 轴, 为坐标原点, 的坐标为 ,反比例函数 的图象的一支过 点,反比例函数 的图象的一支过 点,过 作 轴于 ,若 的面积为 .
(1)求 的值;
(2)求反比例函数 的解析式.

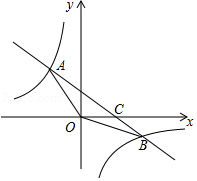
如图,在直角坐标系中,直线 与双曲线 分别相交于第二、四象限内的 , 两点,与 轴相交于 点.已知 , .
(1)求 , 对应的函数表达式;
(2)求 的面积;
(3)直接写出当 时,不等式 的解集.
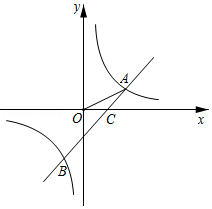
如图,点 为函数 与函数 图象的交点,点 的纵坐标为4, 轴,垂足为点 .
(1)求 的值;
(2)点 是函数 图象上一动点,过点 作 于点 ,若 ,求点 的坐标.

如图,已知反比例函数 与正比例函数 的图象交于 , 两点.
(1)求该反比例函数的表达式;
(2)若点 在 轴上,且 的面积为3,求点 的坐标.

设函数 , .
(1)当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.
(2)设 ,且 ,当 时, ;当 时, .圆圆说:“ 一定大于 ”.你认为圆圆的说法正确吗?为什么?
小明根据学习函数的经验,参照研究函数的过程与方法,对函数 的图象与性质进行探究.
因为 ,即 ,所以可以对比函数 来探究.
列表:(1)下表列出 与 的几组对应值,请写出 , 的值: , ;
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
0 |
|
|
|
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以 相应的函数值为纵坐标,描出相应的点,如图所示:

(2)请把 轴左边各点和右边各点,分别用条光滑曲线顺次连接起来;
(3)观察图象并分析表格,回答下列问题:
①当 时, 随 的增大而 ;(填“增大”或“减小”
②函数 的图象是由 的图象向 平移 个单位而得到.
③函数图象关于点 中心对称.(填点的坐标)
如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于 , 两点,与x轴,y轴分别交于点C,D,连接OA,OB.
(1)求反比例函数 和一次函数 的表达式;
(2)求 的面积.
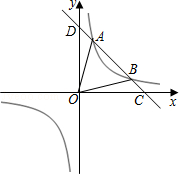
如图,一次函数 的图象与反比例函数 的图象交于点 、 ,与 轴交于点 ,若 ,且 .
(1)求反比例函数与一次函数的表达式;
(2)请直接写出不等式 的解集.
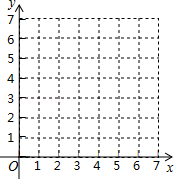
经过实验获得两个变量 , 的一组对应值如下表.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
2.9 |
2 |
1.5 |
1.2 |
1 |
(1)请画出相应函数的图象,并求出函数表达式.
(2)点 , , , 在此函数图象上.若 ,则 , 有怎样的大小关系?请说明理由.
如图,在平面直角坐标系 中,一次函数 的图象分别与 轴、 轴交于点 、 ,与反比例函数 的图象交于点 ,连接 .已知点 , .
(1)求 、 的值;
(2)求 的面积.

如图,一次函数 与反比例函数 的图象交于点 , .
(1)求反比例函数和一次函数的解析式;
(2)判断点 是否在一次函数 的图象上,并说明理由;
(3)写出不等式 的解集.

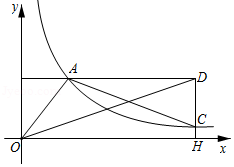
如图, 中, ,顶点 , 都在反比例函数 的图象上,直线 轴,垂足为 ,连结 , ,并延长 交 于点 ,当 时,点 恰为 的中点,若 , .
(1)求反比例函数的解析式;
(2)求 的度数.

已知反比例函数 的图象经过点 .
(1)求该反比例函数的表达式;
(2)如图,在反比例函数 的图象上点 的右侧取点 ,过点 作 轴的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 .
①过点 ,点 分别作 轴, 轴的垂线,两线相交于点 ,求证: , , 三点共线;
②若 ,求证: .
如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .
(1)求反比例函数的解析式;
(2)求 的面积.