经过实验获得两个变量 , 的一组对应值如下表.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
2.9 |
2 |
1.5 |
1.2 |
1 |
(1)请画出相应函数的图象,并求出函数表达式.
(2)点 , , , 在此函数图象上.若 ,则 , 有怎样的大小关系?请说明理由.
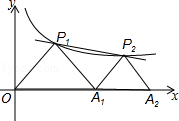
如图, P 1、 P 2是反比例函数 在第一象限图象上的两点,点 A 1的坐标为(4,0).若△ P 1 OA 1与△ P 2 A 1 A 2均为等腰直角三角形,其中点 P 1、 P 2为直角顶点.
(1)求反比例函数的解析式.
(2)①求 P 2的坐标.
②根据图象直接写出在第一象限内当 x满足什么条件时,经过点 P 1、 P 2的一次函数的函数值大于反比例函数 的函数值.
如图,分别位于反比例函数 , 在第一象限图象上的两点 、 ,与原点 在同一直线上,且 .
(1)求反比例函数 的表达式;
(2)过点 作 轴的平行线交 的图象于点 ,连接 ,求 的面积.

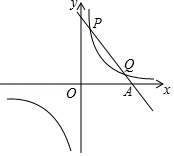
已知一次函数y=k1x+b与反比例函数 的图象交于第一象限内的P( ,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
如图,在平面直角坐标系 中,一次函数 的图象分别与 轴、 轴交于点 、 ,与反比例函数 的图象交于点 ,连接 .已知点 , .
(1)求 、 的值;
(2)求 的面积.

如图,直角三角板ABC放在平面直角坐标系中(AC过O点),直角边AB垂直x轴,垂足为Q,已知∠ACB=60°,点A,C,P均在反比例函数y= 的图象上,分别作PF⊥x轴于F,AD⊥y轴于D,延长DA,FP交于点E,且点P为EF的中点.
的图象上,分别作PF⊥x轴于F,AD⊥y轴于D,延长DA,FP交于点E,且点P为EF的中点.
(1)求点B的坐标;
(2)求四边形AOPE的面积.

如图,一次函数 与反比例函数 的图象在第一象限交于 、 两点, 点的坐标为 ,连接 、 ,过 作 轴,垂足为 ,交 于 ,若 .
(1)求一次函数和反比例函数的表达式;
(2)求 的面积.

如图,反比例函数 y= 与一次函数 y= k 2 x+ b的图象交于 A(2,4), B(﹣4, m)两点.
(1)求 k 1, k 2, b的值;
(2)求△ AOB的面积;
(3)若 M( x 1, y 1), N( x 2, y 2)是反比例函数 y= 的图象上的两点,且 x 1< x 2, y 1< y 2,指出点 M、 N各位于哪个象限.

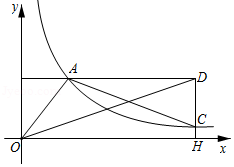
如图, 中, ,顶点 , 都在反比例函数 的图象上,直线 轴,垂足为 ,连结 , ,并延长 交 于点 ,当 时,点 恰为 的中点,若 , .
(1)求反比例函数的解析式;
(2)求 的度数.

如图,一次函数 的图象与 轴、 轴分别交于 , 两点,与反比例函数 的图象分别交于 , 两点,点 ,点 是线段 的中点.
(1)求一次函数 与反比例函数 的解析式;
(2)求 的面积;
(3)直接写出当 取什么值时, .

如图,一次函数 与反比例函数 的图象交于点 , .
(1)求反比例函数和一次函数的解析式;
(2)判断点 是否在一次函数 的图象上,并说明理由;
(3)写出不等式 的解集.

已知反比例函数 的图象经过点 .
(1)求该反比例函数的表达式;
(2)如图,在反比例函数 的图象上点 的右侧取点 ,过点 作 轴的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 .
①过点 ,点 分别作 轴, 轴的垂线,两线相交于点 ,求证: , , 三点共线;
②若 ,求证: .
如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .
(1)求反比例函数的解析式;
(2)求 的面积.
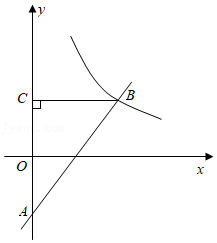
设一次函数 , 是常数, 的图象过 , 两点.
(1)求该一次函数的表达式;
(2)若点 在该一次函数图象上,求 的值.
(3)已知点 , 和点 , 在该一次函数图象上,设 ,判断反比例函数 的图象所在的象限,说明理由.