(本小题满分12分)
已知定义在正实数集上的函数 ,
,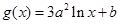 ,其中
,其中 .设两曲线
.设两曲线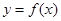 ,
, 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
⑴用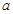 表示
表示 ,并求
,并求 的最大值;
的最大值;
⑵求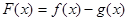 的极值.
的极值.
(本小题满分10分)选修4-4:坐标系与参数方程选讲.
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为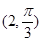 .
.
⑴求圆C的极坐标方程;
⑵ 是圆
是圆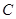 上一动点,点
上一动点,点 满足
满足 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
(本小题满分10分)选修4-5:不等式选讲.
已知函数
⑴解不等式 ;
;
⑵若不等式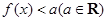 的解集为空集,求
的解集为空集,求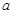 的取值范围.
的取值范围.
如图,在正方体ABCD—A1B1C1D1中,M、N、G分别是A1A,D1C,AD的中点.求证:
(Ⅰ)MN//平面ABCD;
(Ⅱ)MN⊥平面B1BG.
根据市场调查,某商品在最近 的20天内的价格
的20天内的价格 与时间
与时间 满足关系
满足关系
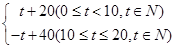 ,销售量
,销售量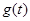 与时间
与时间 满足关系
满足关系 ,
,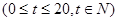 ,设商品的日销售额为
,设商品的日销售额为 (销售量与价格之积).
(销售量与价格之积).
(1 )求商品的日销售额
)求商品的日销售额 的解析式;
的解析式;
(2)求商品的日销售额 的最大值.
的最大值.
如图,A、B、C、D是空间四点,在△ABC中,AB=2,AC=BC= ,等边△ADB所在的平面以AB为轴可转动.
,等边△ADB所在的平面以AB为轴可转动.
(Ⅰ)当平面ADB⊥平面ABC时,求三棱锥 的体积;
的体积;
(Ⅱ)当△ADB转动过程中,是否总有AB⊥CD?请证明你的结论
已知圆 上的动点,点
上的动点,点 在
在 上,且满足|
上,且满足| |=|
|=| |
|
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)过点(2,0)作直线 ,与曲线
,与曲线 交于
交于 、
、 两点,
两点, 是坐标原点,设
是坐标原点,设 是否存在这样的直线
是否存在这样的直线 ,使四边形
,使四边形 的对角线相等(即|
的对角线相等(即| |=|
|=| |)?若存在,求出直线
|)?若存在,求出直线 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
(本小题14分)如图所示,L是海面上一条南北方向的海防警戒线,在L上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1. 5 km/s.
(1)设A到P的距离为 km,用
km,用 分别表示B、C到P 的距离,并求
分别表示B、C到P 的距离,并求 值;
值;
(2)求静止目标P到海防警戒线L的距离(结果精确到0.01 km)。 
.(本小题满分12分)某小区要建一个面积为500平方米的矩形绿地,四周有小路,绿地长边外路宽5米,短边外路宽9米,怎样设计绿地的长与宽,使绿地和小路所占的总面积最小,并求出最小值。