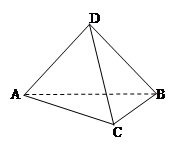如图,A、B、C、D是空间四点,在△ABC中,AB=2,AC=BC=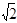 ,等边△ADB所在的平面以AB为轴可转动.
,等边△ADB所在的平面以AB为轴可转动.
(Ⅰ)当平面ADB⊥平面ABC时,求三棱锥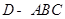 的体积;
的体积;
(Ⅱ)当△ADB转动过程中,是否总有AB⊥CD?请证明你的结论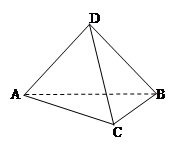
推荐套卷
如图,A、B、C、D是空间四点,在△ABC中,AB=2,AC=BC=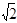 ,等边△ADB所在的平面以AB为轴可转动.
,等边△ADB所在的平面以AB为轴可转动.
(Ⅰ)当平面ADB⊥平面ABC时,求三棱锥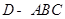 的体积;
的体积;
(Ⅱ)当△ADB转动过程中,是否总有AB⊥CD?请证明你的结论