(12分)设有半径为3 的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.
(本小题满分14分)
设椭圆
 的离心率为
的离心率为 =
= ,点
,点 是椭圆上的一点,
是椭圆上的一点,
且点 到椭圆
到椭圆 两焦点的距离之和为4.
两焦点的距离之和为4.
(1)求椭圆 的方程;
的方程;
(2)椭圆 上一动点
上一动点
 关于直线
关于直线 的对称点为
的对称点为 ,
,
求 的取值范围.
的取值范围.
(本小题满分12分)已知数列 的前n项和为
的前n项和为 等差数列
等差数列 ,又
,又 成等比数列.
成等比数列.
(I)求数列 、
、 的通项公式;
的通项公式;
(II)求数列 的前n项和
的前n项和 .
.
(本小题满分12分)已知函数 ,若存在
,若存在 恒成立,则称
恒成立,则称 的一个“下界函数”.
的一个“下界函数”.
(I)如果函数 的一个“下界函数”,求实数t的取值范围(II)设函数
的一个“下界函数”,求实数t的取值范围(II)设函数 ,试问函数F(x)是否存在零点?若存在,求出零点个数;若不存在,请说明理由.
,试问函数F(x)是否存在零点?若存在,求出零点个数;若不存在,请说明理由.
在直角坐标系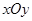 中,点P到两点
中,点P到两点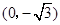 ,
,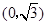 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为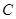 ,直线
,直线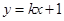 与轨迹C交于A,B两点.
与轨迹C交于A,B两点.
(Ⅰ)写出轨迹C的方程; (Ⅱ)若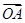
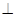
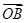 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|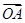 |>|
|>|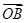 |
|
设椭圆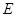 过
过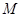 (2,
(2,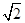 ) ,
) ,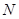 (
( ,1)两点,
,1)两点,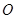 为坐标原点。
为坐标原点。
(1)求椭圆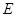 的方程;
的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆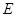 恒有两个交点
恒有两个交点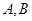 且
且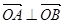 ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求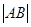 的取值范围,若不存在说明理由。
的取值范围,若不存在说明理由。
甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
| 分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
| 频数 |
2 |
3 |
10 |
15 |
| 分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 频数 |
15 |
x |
3 |
1 |
甲校:
| 分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
| 频数 |
1 |
2 |
9 |
8 |
| 分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 频数 |
10 |
10 |
y |
3 |
乙校:
(Ⅰ)计算x,y的值。
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
| |
甲校 |
乙校 |
总计 |
| 优秀 |
|
|
|
| 非优秀 |
|
|
|
| 总计 |
|
|
|
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异。
| P(k2>k0) |
0.10 |
0.025 |
0.010 |
| K |
2.706 |
5.024 |
6.635 |