(12分)设有半径为3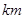
的圆形村落，A、B两人同时从村落中心出发，B向北直行，A先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线前进，后来恰与B相遇.设A、B两人速度一定，其速度比为3：1，问两人在何处相遇？
，
，
，并猜想
，进一步归纳出更一般的结论
，
，
均为正数，且
+
+
在
处的切线与直线
垂直，求
的值
，使得
成立
，求
的最小值
满足
，求证
≥
时，等号成立推荐套卷
(12分)设有半径为3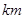的圆形村落，A、B两人同时从村落中心出发，B向北直行，A先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线前进，后来恰与B相遇.设A、B两人速度一定，其速度比为3：1，问两人在何处相遇？
粤公网安备 44130202000953号