在一个盒子中，放有大小相同的红、白、黄三个小球，现从中任意摸出一球，若是红球记1分，白球记2分，黄球记3分．现从这个盒子中有放回地先后摸出两球，所得分数分别记为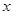
、
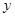，设
为坐标原点，点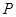
的坐标为
，记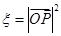
．
(1)求随机变量
=5的概率；
(2)求随机变量的分布列和数学期望．
相关试题
。
，B＝
．
B；⑵求使B
A的实数a的取值范围．
。
时，求曲线
在点
处的切线方程；
时，讨论
的单调性.推荐套卷
在一个盒子中，放有大小相同的红、白、黄三个小球，现从中任意摸出一球，若是红球记1分，白球记2分，黄球记3分．现从这个盒子中有放回地先后摸出两球，所得分数分别记为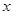、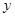，设为坐标原点，点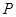的坐标为，记．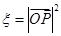
(1)求随机变量=5的概率；
(2)求随机变量的分布列和数学期望．
粤公网安备 44130202000953号