高中数学解答题

记的展开式中，的系数为，的系数为,其中
(1)求（2）是否存在常数p,q(p<q),使，对，恒成立？证明你的结论.

已知函数.
（1）若函数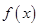在内单调递增，求的取值范围；
（2）若函数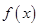在处取得极小值，求的取值范围.

已知函数（）．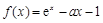
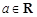（1）当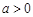时，求函数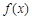的单调区间；
（2）函数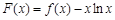在定义域内是否存在零点？若存在，请指出有几个零点；若不存在，请说明理由；
（3）若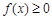对任意恒成立，求a的取值范围．

如图，已知圆E ，点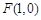，P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．
（1）求动点Q的轨迹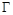的方程；
（2）点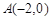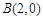，，点G是轨迹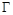上的一个动点，直线AG与直线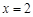相交于点D，试判断以线段BD为直径的圆与直线GF的位置关系，并证明你的结论．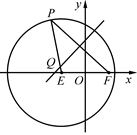

已知数列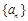的前n项和为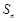满足：．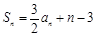
（1）求证：数列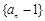是等比数列；
（2）令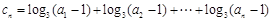，对任意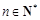，是否存在正整数m，使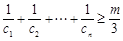都成立？若存在，求出m的值；若不存在，请说明理由．

已知函数（）．
（1）求函数的单调区间；
（2）函数在定义域内是否存在零点？若存在，请指出有几个零点；若不存在，请说明理由；
（3）若，当时，不等式恒成立，求a的取值范围．

已知函数，，其中m∈R．
（1）若0<m≤2，试判断函数f (x)=f₁ (x)+f₂ (x)的单调性，并证明你的结论；
（2）设函数 若对任意大于等于2的实数x₁，总存在唯一的小于2的实数x₂，使得g (x₁) =" g" (x₂) 成立，试确定实数m的取值范围．

已知数列，满足，，，数列的前项和为，.
（1）求数列的通项公式；
（2）求证：；
（3）求证：当时，．

在平面直角坐标系中，如图，已知椭圆E：的左、右顶点分别为、，上、下顶点分别为、．设直线的倾斜角的正弦值为，圆与以线段为直径的圆关于直线对称．

（1）求椭圆E的离心率；
（2）判断直线与圆的位置关系，并说明理由；
（3）若圆的面积为，求圆的方程．

已知函数，，其中m∈R．
（1）若0<m≤2，试判断函数f (x)=f₁ (x)+f₂ (x)的单调性，并证明你的结论；
（2）设函数 若对任意大于等于2的实数x₁，总存在唯一的小于2的实数x₂，使得g (x₁) =" g" (x₂) 成立，试确定实数m的取值范围．

已知数列，满足，，，数列的前项和为，.
（1）求数列的通项公式；
（2）求证：；
（3）求证：当时，．

已知集合，若该集合具有下列性质的子集：每个子集至少含有2个元素，且每个子集中任意两个元素之差的绝对值大于1，则称这些子集为子集，记子集的个数为．
（1）当时，写出所有子集；
（2）求；
（3）记，求证：

已知函数，其中为实数.
(1)当时，求函数在区间上的最大值和最小值；
(2)若对一切的实数，有恒成立，其中为的导函数，求实数的取值范围.

已知函数在上的最大值为
求数列的通项公式；
求证：对任何正整数，都有；
设数列的前项和，求证：对任何正整数，都有成立

已知函数（为实常数）．
（1）若函数在区间上是增函数，试用函数单调性的定义求实数的取值范围；
（2）设，若不等式在有解，求的取值范围．