已知函数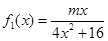
，，其中m∈R．
（1）若0<m≤2，试判断函数f (x)=f1 (x)+f2 (x)
的单调性，并证明你的结论；
（2）设函数
若对任意大于等于2的实数x1，总存在唯一的小于2的实数x2，使得g (x1) =" g" (x2) 成立，试确定实数m的取值范围．
相关试题
于
两点.
与
的值；（2）求证：
.
中， AB=1，
，
.
；
—B的余弦值。
：“函数
在
上单调递减”，命题
：“
，
”，若命题“
的取值范围.
中，已知DA=DC=4,DD1=3,求异面直线A1B与B1C所成角的余弦值。
，过坐标原点O作两条互相垂直的射线，与椭圆分别交于A，B两点．推荐套卷
已知函数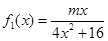，，其中m∈R．
（1）若0<m≤2，试判断函数f (x)=f1 (x)+f2 (x)的单调性，并证明你的结论；
（2）设函数 若对任意大于等于2的实数x1，总存在唯一的小于2的实数x2，使得g (x1) =" g" (x2) 成立，试确定实数m的取值范围．
粤公网安备 44130202000953号