安徽省皖北协作区高三年级联考文科数学试卷
设 是不同的直线,
是不同的直线, 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①若 则
则
②若 则
则
③若 则
则
④若 则
则
其中真命题的序号是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
来源:2014届安徽省皖北协作区高三年级联考文科数学试卷
若 ,且
,且
 则“
则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要 |
来源:2014届安徽省皖北协作区高三年级联考文科数学试卷
某公司为改善职工的出行条件,随机抽取50名职工,调查他们的居住地与公司的距离 [单位:千米].若样本数据分组为
[单位:千米].若样本数据分组为 ,
,  ,
,  ,
,  ,
,  ,
,  , 有数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司的距离不超过4千米的人数为__________.
, 有数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司的距离不超过4千米的人数为__________.
来源:2014届安徽省皖北协作区高三年级联考文科数学试卷
空间中任意放置的棱长为2的正四面体 .下列命题正确的是_________.(写出所有正确的命题的编号)
.下列命题正确的是_________.(写出所有正确的命题的编号)
①正四面体 的主视图面积可能是
的主视图面积可能是 ;
;
②正四面体 的主视图面积可能是
的主视图面积可能是 ;
;
③正四面体 的主视图面积可能是
的主视图面积可能是 ;
;
⑤正四面体 的主视图面积可能是
的主视图面积可能是
⑥正四面体 的主视图面积可能是
的主视图面积可能是 .
.
来源:2014届安徽省皖北协作区高三年级联考文科数学试卷
一袋中装有4个形状、大小完全相同的球,其中黑球2个,白球2个,假设每个小球从袋中被取出的可能性相同,首相由甲取出2个球,并不在将他们原袋中,然后由乙取出剩下的2个球.规定取出一个黑球记1分,取出一个白球记2分,取出球的总积分多者获胜.
(1)求甲、乙平局的概率;
(2)假设可以选择取球的先后顺序,应选择先取,还是后取,请说明理由.
来源:2014届安徽省皖北协作区高三年级联考文科数学试卷
已知函数 ,其中
,其中 为实数.
为实数.
(1)当 时,求函数
时,求函数 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(2)若对一切的实数 ,有
,有 恒成立,其中
恒成立,其中 为
为 的导函数,求实数
的导函数,求实数 的取值范围.
的取值范围.
来源:2014届安徽省皖北协作区高三年级联考文科数学试卷
如图,底面 是边长为2的菱形,且
是边长为2的菱形,且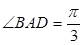 ,以
,以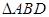 与
与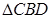 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥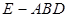 与
与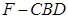 ,且
,且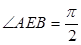 .
.
(1)求证: 平面
平面 ;
;
(2)求多面体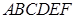 的体积.
的体积.
来源:2014届安徽省皖北协作区高三年级联考文科数学试卷
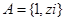 ,
,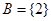 ,
, 为虚数单位,若
为虚数单位,若 ,则纯虚数
,则纯虚数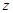 为( )
为( )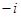
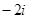

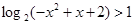 的解集为( )
的解集为( )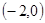

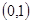
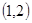
 的焦点是双曲线
的焦点是双曲线 的一个焦点,则正数
的一个焦点,则正数 等于( )
等于( )



 ,则下列关系正确的是( )
,则下列关系正确的是( )



 值为
值为 时,则输出
时,则输出 的值为 ( )
的值为 ( )
 的一条切线与
的一条切线与 轴、
轴、 轴分别交于点
轴分别交于点 , 则
, 则 的最小值为( )
的最小值为( )
 满足不等式组
满足不等式组 ,若
,若 的最大值为
的最大值为 ,最小值为
,最小值为 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



 是定义在
是定义在 上的奇函数,对任意
上的奇函数,对任意 ,都有
,都有 ,若
,若 ,则( )
,则( )



 的前
的前 项积为
项积为 ,若
,若 ,则
,则 =__________.
=__________. ,若关于
,若关于 的函数
的函数 有两个零点, 则实数
有两个零点, 则实数 的取值范围是__________.
的取值范围是__________. 分别为
分别为 三个内角A、B、C的对边,若
三个内角A、B、C的对边,若 ,则
,则 =_________.
=_________.
 的最小正周期;
的最小正周期; ,求
,求 的值域.
的值域. 的公差
的公差 大于0,
大于0, 是方程
是方程 的两根.
的两根. ,求数列
,求数列 的前
的前 项和.
项和.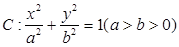 ,过点
,过点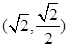 且离心率为
且离心率为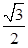 .
.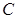 的方程;
的方程;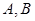 是椭圆
是椭圆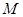 满足
满足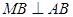 ,连接
,连接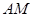 角椭圆于点
角椭圆于点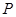 ,在
,在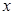 轴上是否存在异于点
轴上是否存在异于点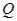 ,使得以
,使得以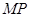 为直径的圆经过直线
为直径的圆经过直线 和直线
和直线 的交点,若存在,求出
的交点,若存在,求出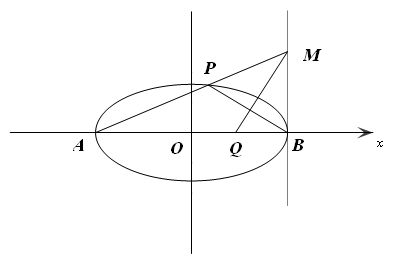
 粤公网安备 44130202000953号
粤公网安备 44130202000953号