某公司近年来科研费用支出x万元与公司所获得利润y万元之间有如下的统计数据:
| x |
2 |
3 |
4 |
5 |
| Y |
18 |
27 |
32 |
35 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 =
= x+
x+ ;
;
(Ⅱ)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:若变量x和y用最小二乘法求出y关于x的线性回归方程为: =
= x+
x+ ,其中:
,其中: =
= ,
, =
= ﹣
﹣
 ,参考数值:2×18+3×27+4×32+5×35=420.
,参考数值:2×18+3×27+4×32+5×35=420.
已知椭圆 :
: 的离心率为
的离心率为 ,一条准线
,一条准线 .
.
(1)求椭圆 的方程;
的方程;
(2)设 为坐标原点,
为坐标原点, 是
是 上的点,
上的点, 为椭圆
为椭圆 的右焦点,过点
的右焦点,过点 作
作 的垂线与以
的垂线与以 为直径的圆
为直径的圆 交于
交于 两点.
两点.
①若 =
= ,求圆
,求圆 的方程;
的方程;
②若 是
是 上的动点,求证:点
上的动点,求证:点 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
是否存在一个等比数列 同时满足下列三个条件:
同时满足下列三个条件:
① 且
且 ;
;
② ;
;
③至少存在一个 ,使得
,使得 依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
| 作物产量(kg) |
300 |
500 |
| 概率 |
0.5 |
0.6 |
| 作物市场价格(元/kg) |
6 |
10 |
| 概率 |
0.4 |
0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
设F1,F2分别是椭圆C: 的左、右焦点.
的左、右焦点.
(1)设点 是椭圆C上的点,且F1(﹣1,0),F2(1,0),试写出椭圆C的方程;
是椭圆C上的点,且F1(﹣1,0),F2(1,0),试写出椭圆C的方程;
(2)设K是(1)中所得椭圆上的动点,求线段 的中点B的轨迹方程;
的中点B的轨迹方程;
(3)设点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M、N两点,若直线PM,PN的斜率都存在,并记为 ,试探究
,试探究 的值是否与点P及直线L有关,并证明你的结论.
的值是否与点P及直线L有关,并证明你的结论.
已知函数f (x)= +ax
+ax 
(1)若f (x)在 x =0处取极值,求a的值,
(2)讨论f(x)的单调性,
(3)证明 ,( e为自然对数的底数,
,( e为自然对数的底数,  )
)
已知点 (0,
(0, ),椭圆
),椭圆 :
: 的离心率为
的离心率为 ,
, 是椭圆的焦点,直线
是椭圆的焦点,直线 的斜率为
的斜率为 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)求 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线 与
与 相交于
相交于 两点,当
两点,当 的面积最大时,求
的面积最大时,求 的方程.
的方程.
设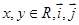 分别为直角坐标系中与
分别为直角坐标系中与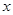 轴、
轴、 轴正半轴同方向的单位向量,若向量
轴正半轴同方向的单位向量,若向量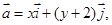
 且
且 .
.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设抛物线 的顶点为
的顶点为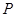 ,焦点为
,焦点为 .直线
.直线 过点
过点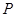 与曲线
与曲线 交于
交于 两点,是否存在这样的直线
两点,是否存在这样的直线 ,使得以
,使得以 为直径的圆过点
为直径的圆过点 ,若存在,求出直线方程;若不存在,请说明理由?
,若存在,求出直线方程;若不存在,请说明理由?
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 ,最小值为
,最小值为 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且线段
,且线段 的垂直平分线过定点
的垂直平分线过定点 ,求
,求 的取值范围。
的取值范围。