(本小题12分)
在某次高三质检考试后,抽取了九位同学的数学成绩进行统计,下表是九位同学的选择题和填空题的得分情况:
| 选择题 |
40 |
55 |
50 |
45 |
50 |
40 |
45 |
60 |
40 |
| 填空题 |
12 |
16 |
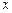  |
12 |
16 |
12 |
8 |
12 |
8 |
(Ⅰ)若这九位同学填空题得分的平均分为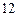 ,试求表中
,试求表中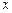 的值及他们填空题得分的标准差;
的值及他们填空题得分的标准差;
(Ⅱ)在(Ⅰ)的条件下,记这九位同学的选择题得分组成的集合为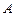 ,填空题得分组成的集合为
,填空题得分组成的集合为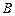 .若同学甲的解答题的得分是
.若同学甲的解答题的得分是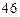 ,现分别从集合
,现分别从集合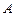 、
、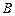 中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于
中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于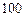 分的概率
分的概率
(本小题12分)
已知数列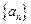 满足
满足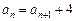 ,
,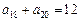 ,等比数列
,等比数列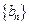 的首项为2,公比为
的首项为2,公比为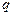 。
。
(Ⅰ)若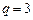 ,问
,问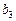 等于数列
等于数列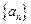 中的第几项?
中的第几项?
(Ⅱ)数列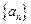 和
和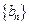 的前
的前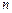 项和分别记为
项和分别记为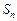 和
和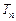 ,
,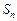 的最大值为
的最大值为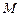 ,当
,当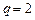 时,试比较
时,试比较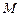 与
与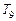 的大小
的大小
(本小题12分)
已知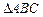 中,角
中,角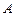 、
、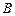 、
、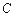 的对边分别为
的对边分别为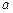 、
、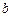 、
、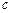 ,
,
角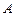 不是最大角,
不是最大角,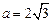 ,外接圆的圆心为
,外接圆的圆心为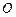 ,半径为
,半径为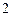 。
。
(Ⅰ)求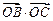 的值;
的值;
(Ⅱ)若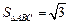 ,求
,求 的周长。
的周长。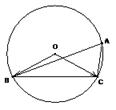
本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知向量 =
=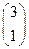 ,变换T的矩阵为A=
,变换T的矩阵为A=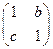 ,平面上的点P(1,1)在变换T
,平面上的点P(1,1)在变换T
作用下得到点P′(3,3),求A4 .
.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
直线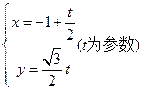 与圆
与圆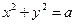 (
(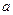 >0)相交于A、B两点,设
>0)相交于A、B两点,设
P(-1,0),且|PA|:|PB|=1:2,求实数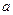 的值
的值
(3)(本小题满分7分)选修4-5:不等式选讲
对于x∈R,不等式|x-1|+|x-2|≥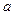 2+
2+ 2恒成立,试求2
2恒成立,试求2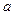 +
+ 的最大值。
的最大值。
(本小题满分14分)已知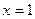 是函数
是函数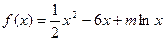 的一个极值点。
的一个极值点。
(Ⅰ)求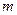 ;
;
(Ⅱ)若直线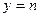 与函数
与函数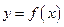 的图象有3个交点,求
的图象有3个交点,求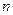 的取值范围;
的取值范围;
(Ⅲ)设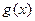 =(
=(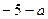 )
)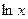 +
+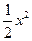 +(6-
+(6-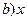 +2(
+2(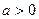 ),
),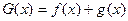 ,若
,若 =0有两个零点
=0有两个零点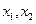 ,且
,且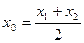 ,试探究
,试探究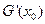 值的符号
值的符号
(本小题满分13分)已知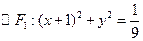 、
、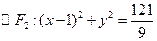 ,椭圆C的方程为
,椭圆C的方程为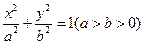 ,
,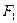 、
、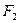 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设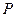 为椭圆C上一点,存在以
为椭圆C上一点,存在以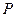 为圆心的
为圆心的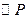 与
与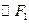 外切、与
外切、与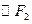 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点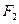 作斜率为
作斜率为 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与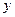 轴相交于点D,若
轴相交于点D,若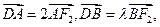 求
求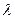 的值;
的值;
(Ⅲ)已知真命题:“如果点T(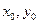 )在椭圆
)在椭圆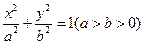 上,那么过点T
上,那么过点T
的椭圆的切线方程为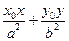 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线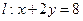 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
(本小题满分13分)如图,由不大于n(n∈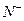 )的正有理数排成的数表,质点按
)的正有理数排成的数表,质点按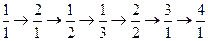
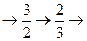 ……顺序跳动,
……顺序跳动,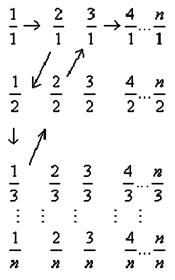
所经过的有理数依次排列构成数列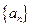 。
。
(Ⅰ)质点从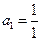 出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从
出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从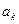 到达
到达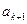 );骰子的点数为偶数时,质点往前跳二步(从
);骰子的点数为偶数时,质点往前跳二步(从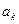 到达
到达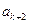 ).
).
①抛掷骰子二次,质点到达的有理数记为ξ,求Eξ;②求质点恰好到达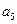 的概率。
的概率。
(Ⅱ)试给出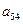 的值(不必写出求解过程)。
的值(不必写出求解过程)。
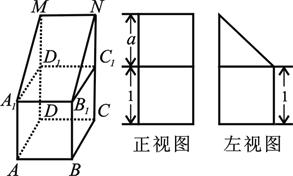
(本小题满分13分)如图,在正方体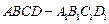 的上底面上叠放三棱柱
的上底面上叠放三棱柱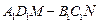 ,该几何体的正视图与左视图如右图所示.
,该几何体的正视图与左视图如右图所示.
(Ⅰ)若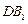
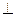
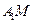 ,求实数
,求实数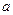 的值;
的值;
(Ⅱ)在(I)的条件下:
① 证明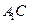
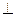 平面
平面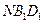 ;
;
②求直线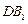 与平面
与平面 所成角的正弦值
所成角的正弦值
(本小题满分13分)已知向量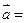
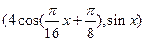 ,
,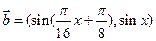 ,
,
定义函数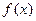 =
=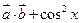 。
。
(Ⅰ)求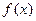 的最小正周期;在所给的坐标系中作出函数
的最小正周期;在所给的坐标系中作出函数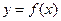 ,
,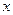 ∈
∈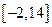 的图象
的图象
(不要求写出作图过程);
(Ⅱ)若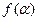 =2,且14≤
=2,且14≤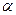 ≤18,求
≤18,求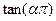 的值
的值
(满分12分)直线l 与抛物线y2 = 4x 交于两点A、B,O 为原点,且 = -4.
= -4.
(I) 求证:直线l 恒过一定点;
(II) 若 4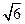 ≤| AB | ≤
≤| AB | ≤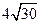 ,求直线l 的
,求直线l 的 斜率k 的取值范围;
斜率k 的取值范围;
(Ⅲ) 设抛物线的焦点为F,∠AFB = θ,试问θ 角 能否
能否 等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.
等于120°?若能,求出相应的直线l 的方程;若不能,请说明理由.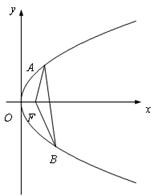
(满分12分)设f (x) 是定义在 [-1,1] 上的偶函数,f (x) 与g(x) 的图象关于x =" 1" 对称,且当x Î [2,3] 时,g(x) = a (x-2)-2 (x-2) 3(a 为常数).
 (Ⅰ)求f (x) 的解析式;
(Ⅰ)求f (x) 的解析式;
(Ⅱ)若f (x) 在 [0,1] 上是增函数,求实数a 的取值范围;
(Ⅲ)若a  Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
(满分12分)某专卖店销售一新款服装,日销售量(单位为件)f (n) 与时间n(1≤n≤30、nÎ N*)的函数关系如下图所示,其中函数f (n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
(Ⅰ)求f (n) 的表达式,及前m天的销售总数;
(Ⅱ)按以往经验,当该专卖店销售某款服装的总数超过 400 件时,市面上会流行该款服装,而日销售量连续下降并低于 30 件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过 10 天?请说明理由.

(满分12 分)某班有两个课外活动小组,其中第一小组有足球票6张,排球票 4张;第二小组有足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,和乙从第二小组的10张票中任抽1张.
分)某班有两个课外活动小组,其中第一小组有足球票6张,排球票 4张;第二小组有足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,和乙从第二小组的10张票中任抽1张.
(Ⅰ)两人都抽到足球票的概率是多少?
(Ⅱ)两人中至少有1人抽到足球票的概率是多少?