福建省龙岩市高三第二次质检数学试题(文)
下方左图表示一个由相同小 立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则该几何体的正视图为
立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则该几何体的正视图为
A B C D
设 是三个互不重合的平面,
是三个互不重合的平面, 是两条不重合的直线,则下列命题中正确的是( )
是两条不重合的直线,则下列命题中正确的是( )
A.若 ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
如果一个点是一个指数函数和一个对数函数的图像的交点,那么称这个点为“好点”。下列五个点 ,
, ,
, ,
, ,
, 中,“好点”是 (写出所有的好点)。
中,“好点”是 (写出所有的好点)。
(本小题12分)
已知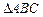 中,角
中,角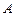 、
、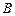 、
、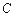 的对边分别为
的对边分别为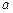 、
、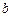 、
、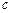 ,
,
角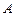 不是最大角,
不是最大角,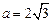 ,外接圆的圆心为
,外接圆的圆心为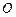 ,半径为
,半径为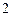 。
。
(Ⅰ)求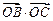 的值;
的值;
(Ⅱ)若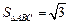 ,求
,求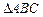 的周长。
的周长。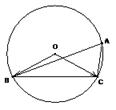
(本小题12分)
已知数列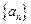 满足
满足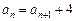 ,
,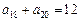 ,等比数列
,等比数列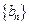 的首项为2,公比为
的首项为2,公比为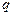 。
。
(Ⅰ)若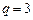 ,问
,问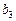 等于数列
等于数列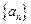 中的第几项?
中的第几项?
(Ⅱ)数列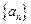 和
和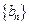 的前
的前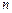 项和分别记为
项和分别记为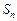 和
和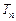 ,
,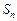 的最大值为
的最大值为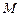 ,当
,当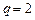 时,试比较
时,试比较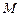 与
与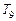 的大小
的大小
(本小题12分)
在某次高三质检考试后,抽取了九位同学的数学成绩进行统计,下表是九位同学的选择题和填空题的得分情况:
| 选择题 |
40 |
55 |
50 |
45 |
50 |
40 |
45 |
60 |
40 |
| 填空题 |
12 |
16 |
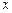  |
12 |
16 |
12 |
8 |
12 |
8 |
(Ⅰ)若这九位同学填空题得分的平均分为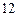 ,试求表中
,试求表中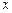 的值及他们填空题得分的标准差;
的值及他们填空题得分的标准差;
(Ⅱ)在(Ⅰ)的条件下,记这九位同学的选择题得分组成的集合为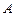 ,填空题得分组成的集合为
,填空题得分组成的集合为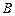 .若同学甲的解答题的得分是
.若同学甲的解答题的得分是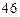 ,现分别从集合
,现分别从集合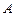 、
、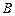 中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于
中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于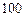 分的概率
分的概率
(本小题12分)
图甲是一个几何体的表面展开图,图乙是棱长为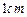 的正方体。
的正方体。
(Ⅰ)若沿图甲中的虚线将四个三角形折叠起来,使点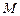 、
、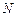 、
、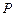 、
、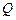 重合,则可以围成怎样的几何体?请求出此几何体的体积;
重合,则可以围成怎样的几何体?请求出此几何体的体积;
(Ⅱ)需要多少个(I)的几何体才能拼成一个图乙中的正方 体?请按图乙中所标字母写出这几个几何体的名称;
体?请按图乙中所标字母写出这几个几何体的名称;
(Ⅲ)在图乙中,点 为棱
为棱 上的动点,试判断
上的动点,试判断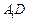 与平面
与平面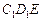 是否垂直,并说明理由。
是否垂直,并说明理由。
(本小题12分)
过椭圆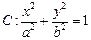
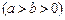 的一个焦点
的一个焦点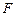 且垂直于
且垂直于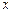 轴的直线交椭圆于点
轴的直线交椭圆于点 。
。
(Ⅰ) 求椭圆C的方程;
求椭圆C的方程;
(Ⅱ)是否存在过点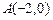 的直线
的直线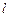 与椭圆
与椭圆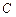 交于两点
交于两点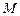 、
、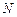 ,使得
,使得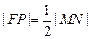 (其中
(其中 为弦
为弦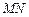 的中点)?若存在,求出直线
的中点)?若存在,求出直线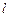 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
 等于
等于



 ,集合
,集合 ,
, ,则
,则 等于
等于



 :
: ,条件
,条件 :
: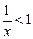 ,则
,则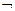
 的前
的前 项和为
项和为 ,且
,且 ,则
,则 等于
等于
 的图象经过点
的图象经过点 ,则
,则 的值等于
的值等于

 的值为
的值为



 的焦点到直线
的焦点到直线 的距离为
的距离为



 的图象向左平移
的图象向左平移 个单位得到的图象关于原点对称,则
个单位得到的图象关于原点对称,则 的值可以为
的值可以为



 与
与 关于
关于 轴对称,
轴对称,
 ,则满足不等式
,则满足不等式
 的点
的点 的集合用阴影表示为下图中的
的集合用阴影表示为下图中的
 、
、 都是定义在
都是定义在 上的函数,
上的函数, ,
, ,
, .在区间
.在区间 上随机取一个数
上随机取一个数 ,
, 的值介于4到8之间的概率是
的值介于4到8之间的概率是



 的离心率为 。
的离心率为 。
 、
、 ,
, 若
若 的运算原理如下图所示,
的运算原理如下图所示, 是函数
是函数 的零点,
的零点, 是二次函数
是二次函数 在
在 上的最大值,则
上的最大值,则 。
。
 为实数,
为实数, 是函数
是函数 的一个极值点。
的一个极值点。 在区间
在区间 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围; ,对于任意
,对于任意 和
和 ,有不等式
,有不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
 粤公网安备 44130202000953号
粤公网安备 44130202000953号