(本小题满分14分)设直线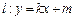 (其中
(其中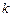 ,
, 为整数)与椭圆
为整数)与椭圆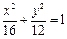 交于不同两点
交于不同两点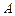 ,
,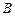 ,与双曲线
,与双曲线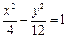 交于不同两点
交于不同两点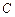 ,
,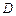 ,问是否存在直线
,问是否存在直线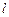 ,使得向量
,使得向量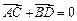 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
在非负数构成的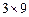 数表
数表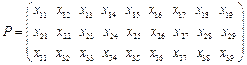
中每行的数互不相同,前6列中每列的三数之和为1,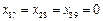 ,
,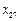 ,
,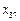 ,
,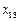 ,
,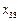 ,
,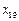 ,
,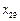 均大于.如果
均大于.如果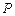 的前三列构成的数表
的前三列构成的数表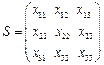
满足下面的性质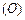 :对于数表
:对于数表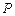 中的任意一列
中的任意一列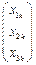 (
(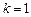 ,2,…,9)均存在某个
,2,…,9)均存在某个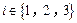
使得
⑶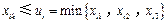 .
.
求证:
(ⅰ)最小值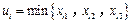 ,
,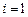 ,2,3一定自数表
,2,3一定自数表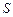 的不同列.
的不同列.
(ⅱ)存在数表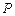 中唯一的一列
中唯一的一列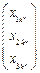 ,
,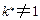 ,2,3使得
,2,3使得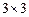 数表
数表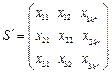
仍然具有性质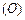 .
.
如图,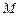 ,
,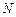 分别为锐角三角形
分别为锐角三角形 (
(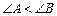 )的外接圆
)的外接圆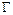 上弧
上弧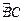 、
、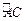 的中点.过点
的中点.过点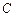 作
作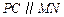 交圆
交圆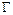 于
于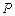 点,
点,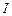 为
为 的内心,连接
的内心,连接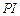 并延长交圆
并延长交圆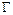 于
于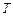 .
.
⑴求证: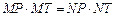 ;
;
⑵在弧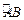 (不含点
(不含点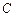 )上任取一点
)上任取一点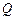 (
(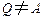 ,
,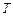 ,
,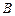 ),记
),记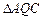 ,
,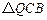 的内心分别为
的内心分别为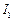 ,
,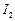 ,
,
求证: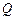 ,
,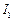 ,
,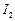 ,
,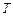 四点共圆.
四点共圆.
(本小题满分14分)
已知函数 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 在区间
在区间 上是减函数.
上是减函数.
(1)求实数 的值;
的值;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 的根的个数。
的根的个数。
(本小题满分12分)
已知一非零向量列 满足:
满足: ,
,
(1)证明: 是等比数列;
是等比数列;
(2)设 ,
, ,求
,求 ;
;
(3)设 ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
(本小题满分12分)
如图,椭圆 经过点
经过点 ,离心率
,离心率 。
。
(l)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 交于
交于 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 与
与 不重合),则直线
不重合),则直线 与
与 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
(本小题满分12分)
经调查某 校高三年级学生家庭月平均收入不多于10000元的共有100
校高三年级学生家庭月平均收入不多于10000元的共有100 0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
某企业准备给该校高三学生发放助学金,发放规定为:家庭收入在4000元以下(≤4000元)的每位同学得助学金2000元,家庭收入在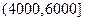 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在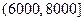 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在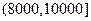 (元)间的同学不发助学金.
(元)间的同学不发助学金.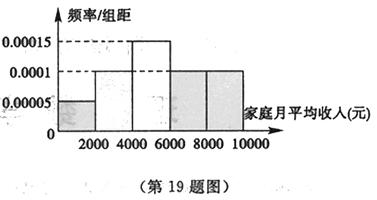
(l)记该年级某位同学所得助学金为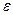 元,写出
元,写出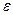 的分布列,并计算该企业发放该年级的助学金约需要的资金;
的分布列,并计算该企业发放该年级的助学金约需要的资金;
(2)记该年级两位同学所得助学金之差的绝对值为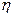 元,求
元,求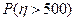 .
.
(本小题满分12分)
如图所示,直三棱柱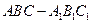 的各条棱长均为
的各条棱长均为 ,
, 是侧棱
是侧棱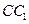 的中点.
的中点.
(l)求证:平面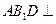 平面
平面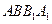 ;
;
(2)求异面直线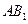 与
与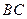 所成角的余弦值;
所成角的余弦值;
(3)求平面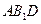 与平面
与平面 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.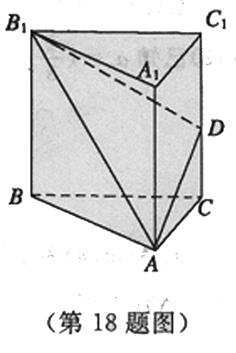
(本小题满分12分)
设函数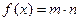 ,其中向量
,其中向量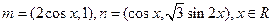 .
.
(1) 求函数
求函数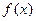 的最
的最 小正周期与单调递减区间;
小正周期与单调递减区间;
(2)在△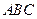 中,
中,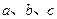 分别是角
分别是角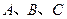
 的对边,已知
的对边,已知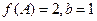 ,△
,△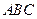 的面积为
的面积为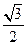 ,求△
,求△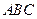 外接圆半径
外接圆半径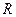 .
.
(本小题满分14分)
设数列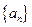 ,
,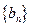 满足:a1=4,a2=
满足:a1=4,a2=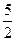 ,
,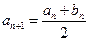 ,
, 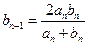 .
.
(1)用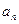 表示
表示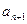 ;并证明:
;并证明: , an>2 ;
, an>2 ;
(2)证明: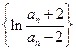 是等比数列;
是等比数列;
(3)设Sn是数列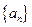 的前n项和,当n≥2时,Sn与
的前n项和,当n≥2时,Sn与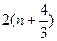 是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
(本小题满分12分)
已知函数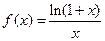 .
.
(1)确定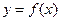 在(0,
在(0, +∞)上的单调性;
+∞)上的单调性;
(2)设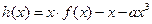 在(0,2)上有极值,求a的取值范围.
在(0,2)上有极值,求a的取值范围.