山东省聊城市高三二模理科数学试题
给出下列命题
①若直线 与平面
与平面 内的一条直线平行,则
内的一条直线平行,则 ∥
∥ ;
;
②若平面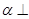 平面
平面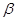 ,且
,且 ,则过
,则过 内一点
内一点 与
与 垂直的直线垂直于平面
垂直的直线垂直于平面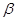 ;
;
③ ;
;
④已知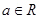 ,则“
,则“ ”是“
”是“ ”的必要不充分条件.
”的必要不充分条件.
其中正确命题的个数是
| A.4 | B.3 | C.2 | D.1 |
将函数 向右平移
向右平移 个单位,再将所得的函数图象上的各点纵坐标不 变,横坐标变为原来的2倍,得到函数
个单位,再将所得的函数图象上的各点纵坐标不 变,横坐标变为原来的2倍,得到函数 的图象,则函数
的图象,则函数 与
与 ,
, ,
, 轴围成的图形面积为
轴围成的图形面积为
A. |
B. |
C. |
D. |
2
(本小题满分12分)
如图所示,直三棱柱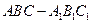 的各条棱长均为
的各条棱长均为 ,
, 是侧棱
是侧棱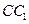 的中点.
的中点.
(l)求证:平面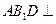 平面
平面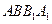 ;
;
(2)求异面直线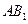 与
与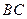 所成角的余弦值;
所成角的余弦值;
(3)求平面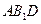 与平面
与平面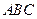 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.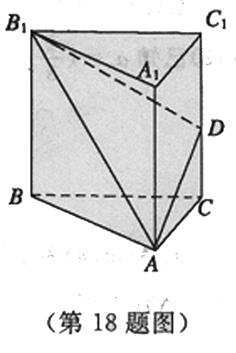
(本小题满分12分)
经调查某 校高三年级学生家庭月平均收入不多于10000元的共有100
校高三年级学生家庭月平均收入不多于10000元的共有100 0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
某企业准备给该校高三学生发放助学金,发放规定为:家庭收入在4000元以下(≤4000元)的每位同学得助学金2000元,家庭收入在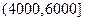 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在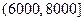 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在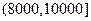 (元)间的同学不发助学金.
(元)间的同学不发助学金.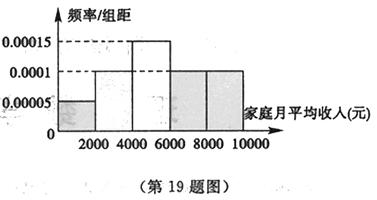
(l)记该年级某位同学所得助学金为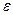 元,写出
元,写出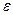 的分布列,并计算该企业发放该年级的助学金约需要的资金;
的分布列,并计算该企业发放该年级的助学金约需要的资金;
(2)记该年级两位同学所得助学金之差的绝对值为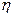 元,求
元,求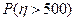 .
.
(本小题满分12分)
如图,椭圆 经过点
经过点 ,离心率
,离心率 。
。
(l)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 交于
交于 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 与
与 不重合),则直线
不重合),则直线 与
与 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
(本小题满分12分)
已知一非零向量列 满足:
满足: ,
,
(1)证明: 是等比数列;
是等比数列;
(2)设 ,
, ,求
,求 ;
;
(3)设 ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
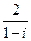 对应的点到直线
对应的点到直线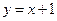 的距离是
的距离是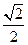
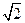

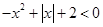 的解集是
的解集是
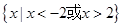
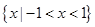
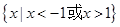
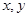 的取值如下表所示:
的取值如下表所示: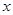
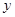
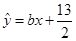 ,则
,则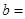
 (B)
(B)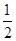 (C)
(C)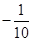 (D)
(D)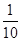
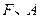 分别为双曲
分别为双曲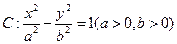 的左焦点、右顶点,点
的左焦点、右顶点,点 满足
满足 ,则双曲线的离心率为
,则双曲线的离心率为
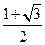
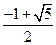

 的正方体
的正方体 内任取一点,则点
内任取一点,则点 到点
到点 的距离小于等于
的距离小于等于




 的零点所在的区间是
的零点所在的区间是 )
) )
) )
) )
) 满足不等式组
满足不等式组 目标函数
目标函数 的最大值为2,则实数
的最大值为2,则实数 的值是
的值是
 为抛物线
为抛物线 上一个动点,
上一个动点, 为圆
为圆 上一个动点,那么点
上一个动点,那么点



 ,把数列
,把数列 的各项排列成如下的三角形状:
的各项排列成如下的三角形状:








 表示第
表示第 行的第
行的第 个数,则
个数,则





 中,
中, ,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是 。
,利用如图所示的程序框图计算该数列的第10项,则判断框中应填的语句是 。
 为三角形
为三角形 的边
的边 的中点,点
的中点,点 满足
满足 ,则实数
,则实数 的值为_______.
的值为_______. 的展开式中
的展开式中 的系数记为
的系数记为 ,则
,则 .
.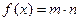 ,其中向量
,其中向量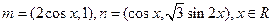 .
. 求函数
求函数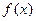 的最
的最 小正周期与单调递减区间;
小正周期与单调递减区间;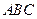 中,
中,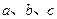 分别是角
分别是角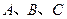
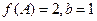 ,△
,△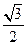 ,求△
,求△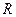 .
. 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 在区间
在区间 上是减函数.
上是减函数. 的值;
的值; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; 的方程
的方程 的根的个数。
的根的个数。 粤公网安备 44130202000953号
粤公网安备 44130202000953号