本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知椭圆 :
: (
(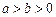 ),其焦距为
),其焦距为 ,若
,若 (
( ),则称椭圆
),则称椭圆 为“黄金椭圆”.
为“黄金椭圆”.
(1)求证:在黄金椭圆 :
: (
(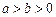 )中,
)中, 、
、 、
、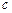 成等比数列.
成等比数列.
(2)黄金椭圆 :
: (
(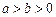 )的右焦点为
)的右焦点为 ,
, 为椭圆
为椭圆 上的
上的
任意一点.是否存在过点 、
、 的直线
的直线 ,使
,使 与
与 轴的交点
轴的交点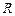 满足
满足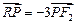 ?若存在,求直线
?若存在,求直线 的斜率
的斜率 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)在黄金椭圆中有真命题:已知黄金椭圆 :
: (
(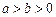 )的左、右
)的左、右
焦点分别是 、
、 ,以
,以 、
、 、
、 、
、 为顶点的菱形
为顶点的菱形 的内切圆过焦点
的内切圆过焦点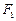 、
、 .
.
试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
本题共有2个小题,第1小题满分8分,第2小题满分8分.
如图,反比例函数 (
( )的图像过点
)的图像过点 和
和 ,点
,点 为该函数图像上一动点,过
为该函数图像上一动点,过 分别作
分别作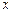 轴、
轴、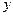 轴的垂线,垂足为
轴的垂线,垂足为 、
、 .记四边形
.记四边形 (
( 为坐标原点)与三角形
为坐标原点)与三角形 的公共部分面积为
的公共部分面积为 .
.
(1)求 关于
关于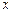 的表达式;
的表达式;
(2)求 的最大值及此时
的最大值及此时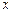 的值.
的值.
 (本题满分1
(本题满分1 4分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
4分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
在长方体 中,
中, ,过
,过 、
、 、
、 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,且这个几何体的体积为
,且这个几何体的体积为 .
.
(1)求棱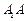 的长;
的长;
(2)求点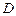 到平面
到平面 的距离.
的距离.

已知关于 的实系数一元二次方程
的实系数一元二次方程 有两个虚根
有两个虚根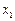 ,
, ,且
,且 (
(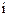
 为虚
为虚 数单位),
数单位), ,求实数
,求实数 的值.
的值.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
从数列 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 的一个子数列.
的一个子数列.
设数列 是一个首项为
是一个首项为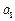 、公差为
、公差为

 的无穷等差数列.
的无穷等差数列.
(1)若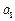 ,
, ,
, 成等比数列,求其公比
成等比数列,求其公比 .
.
(2)若 ,从数列
,从数列 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若 ,从数列
,从数列 中取出第1项、第
中取出第1项、第
 项(设
项(设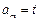 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为 的无穷等比子数列.
的无穷等比子数列.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知椭圆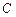 :
: (
( ),其左、右焦点分别为
),其左、右焦点分别为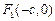 、
、 ,且
,且 、
、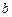 、
、 成等比数列.
成等比数列.
(1)求 的值.
的值.
(2)若椭圆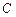 的上顶点、右顶点分别为
的上顶点、右顶点分别为 、
、 ,求证:
,求证: .
.
(3)若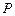 为椭圆
为椭圆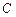 上的任意一点,是否存在过点
上的任意一点,是否存在过点 、
、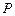 的直线
的直线 ,使
,使 与
与 轴的交点
轴的交点 满足
满足 ?若存在,求直线
?若存在,求直线 的斜率
的斜率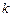 ;若不存在,请说明理由.
;若不存在,请说明理由.
本题共有2个小题,第1小题满分8分,第2小题满分8分.
如图,反比例函数 (
( )的图像过点
)的图像过点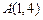 和
和 ,点
,点 为该函数图像上一动点,过
为该函数图像上一动点,过 分别作
分别作 轴、
轴、 轴的垂线,垂足为
轴的垂线,垂足为 、
、 .记四边形
.记四边形 (
( 为坐标原点)与三角形
为坐标原点)与三角形 的公共部分面积为
的公共部分面积为 .
.
(1)求 关于
关于 的表达式;
的表达式;
(2)求 的最大值及此时
的最大值及此时 的值.
的值.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
在长方体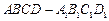 中,
中, ,过
,过 、
、 、
、 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,且这个几何体的体积为
,且这个几何体的体积为 .
.
(1)求棱 的长;
的长;
(2)若 的中点为
的中点为 ,求异面直线
,求异面直线 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).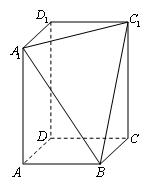
已知关于 的实系数一元二次方程
的实系数一元二次方程 有两个虚根
有两个虚根 ,
, ,且
,且 (
( 为虚数单位),
为虚数单位), ,求实数
,求实数 的值.
的值.
(本题满分18分;第(1)小题4分,第(2)小题6分,第(3)小题8分)
设数列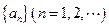 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列 中任意(不同)两项之和仍是该数列中的一项,则
中任意(不同)两项之和仍是该数列中的一项,则 称该数列是“封闭数列”.
称该数列是“封闭数列”.
(1)若 ,判断该数列是否为“封闭数列”,并说明理由?
,判断该数列是否为“封闭数列”,并说明理由?
(2)设 是数列
是数列 的前
的前 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使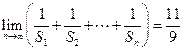 ;若存
;若存 在,求
在,求 的通项公式,若不存在,说明理由;
的通项公式,若不存在,说明理由;
(3)试问:数列 为“封闭数列”的充要条件是什么?给出你的结论并加以证明.
为“封闭数列”的充要条件是什么?给出你的结论并加以证明.
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设 、
、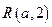 为坐标平面
为坐标平面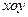 上的点,直线
上的点,直线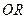 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线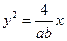 交于点
交于点 (异于
(异于 ).
).
(1) 若对任意
 ,点
,点 在抛物线
在抛物线 上,试问当
上,试问当 为何值时,点
为何值时,点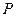 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
;
(2) 若点 在椭圆
在椭圆 上,试问:点
上,试问:点 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3) 对(1)中点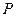 所在圆方程
所在圆方程 ,设
,设 、
、 是圆
是圆 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆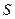 ,使直线
,使直线 恒与圆
恒与圆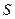 相切.
相切.
(满分16分;第(1)小题5分,第(2)小题5分,第三 小题6分)
小题6分)
已知函数 
(1)判断并证明 在
在 上的单调性;
上的单调性;
(2)若存在 ,使
,使 ,则称
,则称 为函数
为函数 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求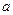 的值,并求出不动点
的值,并求出不动点 ;
;
(3)若 在
在 上恒成立 , 求
上恒成立 , 求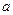 的取值范围.
的取值范围.
(如图)已知正方体
 的棱长均为1,
的棱长均为1, 为棱
为棱 上的点,
上的点, 为棱
为棱 的中点,异面直线
的中点,异面直线 与
与 所成角的大小为
所成角的大小为 ,求
,求 的值.
的值. 
(本题满分18分;第(1)小题5分,第(2)小题5分,第(3)小题8分)
设数列 是等差数列,且公差为
是等差数列,且公差为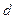 ,若数列
,若数列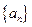 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
(1)若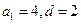 ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”;
(2)试判断数列 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么?
(3)设 是数列
是数列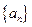 的前
的前 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使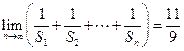 ;若存在,求
;若存在,求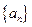 的通项公式,若不存在,说明理由.
的通项公式,若不存在,说明理由.