上海市徐汇区高三第二次模拟考试数学卷(理)
有5只苹果,它们的质量分别为125  121
121 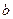 127(单位:克):若该样本的中位数和平均值均为
127(单位:克):若该样本的中位数和平均值均为 ,则该样本的标准差
,则该样本的标准差 =_____________.(克)(用数字作答)
=_____________.(克)(用数字作答)
在极坐标系中,若过点(3,0)且与极轴垂直的直线交曲线 于A、B两点,则
于A、B两点,则 ="______________________."
="______________________."
某学生参加一次世博志愿者测试,已知在备选的10道试题中,预计每道题该学生答对的概率为 。规定每位考生都从备选题中随机抽出3道题进行测试,则该学生仅答对2道题的概率是______________.(用数值表示)
。规定每位考生都从备选题中随机抽出3道题进行测试,则该学生仅答对2道题的概率是______________.(用数值表示)
复数 等于-------------------------------------------------------------------------( )
等于-------------------------------------------------------------------------( )
A. B.
B. C
C .
. D.
D.
下列函数中,与函数 有相同定义域的是-----------------------------( )
有相同定义域的是-----------------------------( )
A. |
B. |
C. |
D. |
设P是△ABC所在平面内的一点, ,则-----------------( )
,则-----------------( )
A. |
B. |
C. |
D. |
已知 为圆
为圆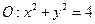 的两条互相垂直的弦,
的两条互相垂直的弦, 交于点
交于点 ,则四边形
,则四边形 面积的最大值为----------------------------------------------------------------( )
面积的最大值为----------------------------------------------------------------( )
A 4 B 5 C 6 D 7
(满分16分;第(1)小题5分,第(2)小题5分,第三 小题6分)
小题6分)
已知函数 
(1)判断并证明 在
在 上的单调性;
上的单调性;
(2)若存在 ,使
,使 ,则称
,则称 为函数
为函数 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求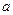 的值,并求出不动点
的值,并求出不动点 ;
;
(3)若 在
在 上恒成立 , 求
上恒成立 , 求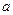 的取值范围.
的取值范围.
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设 、
、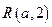 为坐标平面
为坐标平面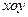 上的点,直线
上的点,直线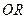 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线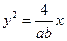 交于点
交于点 (异于
(异于 ).
).
(1) 若对任意
 ,点
,点 在抛物线
在抛物线 上,试问当
上,试问当 为何值时,点
为何值时,点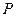 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
;
(2) 若点 在椭圆
在椭圆 上,试问:点
上,试问:点 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3) 对(1)中点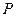 所在圆方程
所在圆方程 ,设
,设 、
、 是圆
是圆 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆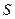 ,使直线
,使直线 恒与圆
恒与圆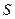 相切.
相切.
 ,则
,则 _______________.
_______________.  ,则
,则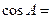 _______________.
_______________.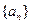 满足:
满足: ,则前6项的和
,则前6项的和 .
. 的展开式中
的展开式中 的系数为_____________.
的系数为_____________. ,则它们的半径之比
,则它们的半径之比 =_____________.
=_____________.  的反函数为________________.
的反函数为________________. 第2行第1列元素的代数余子式为
第2行第1列元素的代数余子式为 ,则
,则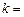 ____________.
____________. 的焦点为
的焦点为 ,点P在椭圆上,若
,点P在椭圆上,若 ,则
,则 的大小为____________
的大小为____________ ___.
___. 中,已知
中,已知 ,
, ,则
,则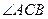 的最大值为_______________.
的最大值为_______________. 时,集合
时,集合 有且只有3个整数,则
有且只有3个整数,则 的取值范围是___________.
的取值范围是___________. 表示不超过
表示不超过 的最大整数,如
的最大整数,如 .
. ,则
,则 的值域为________________.
的值域为________________. 中,
中, 、
、 、
、 是
是 、
、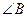 、
、 的对边,已知
的对边,已知 ,
, ,
, ,求
,求 .
.
 的棱长均为1,
的棱长均为1, 为棱
为棱 上的点,
上的点, 为棱
为棱 的中点,异面直线
的中点,异面直线 与
与 所成角的大小为
所成角的大小为 ,求
,求 的值.
的值. 
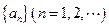 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列 中任意(不同)两项之和仍是该数列中的一项,则
中任意(不同)两项之和仍是该数列中的一项,则 称该数列是“封闭数列”.
称该数列是“封闭数列”. ,判断该数列是否为“封闭数列”,并说明理由?
,判断该数列是否为“封闭数列”,并说明理由? 是数列
是数列 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使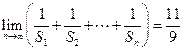 ;若存
;若存 在,求
在,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号