(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设 、
、 为坐标平面
为坐标平面 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点 (异于
(异于 ).
).
(1) 若对任意
 ,点
,点 在抛物线
在抛物线 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
;
(2) 若点 在椭圆
在椭圆 上,试问:点
上,试问:点 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3) 对(1)中点 所在圆方程
所在圆方程 ,设
,设 、
、 是圆
是圆 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 相切.
相切.
相关知识点
推荐套卷
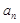 的信息如下图。
的信息如下图。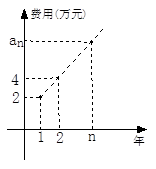
 , q:x2-2x+1-m2≤0(m>0),若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.
, q:x2-2x+1-m2≤0(m>0),若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.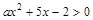 的解集是
的解集是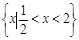 ,求不等式
,求不等式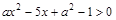 的解集.
的解集. ,试比较
,试比较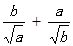 与
与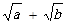 的大小。
的大小。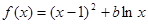 ,其中
,其中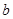 为常数.
为常数.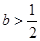 时,判断函数
时,判断函数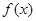 在定义域上的单调性;
在定义域上的单调性; 粤公网安备 44130202000953号
粤公网安备 44130202000953号