已知椭圆C: ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2, ,离心率
,离心率 .过直线l:
.过直线l: 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B.
(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x0,y0)处的切线方程为:x0x+y0y=r2”.由上述结论类比得到:“过椭圆 (a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(2)利用(1)中的结论证明直线AB恒过定点( );
);
(3)当点M的纵坐标为1时,求△ABM的面积.
(本小题满分12分)为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
| 组别 |
候车时间 |
人数 |
| 一 |
 |
2 |
| 二 |
 |
6 |
| 三 |
 |
4 |
| 四 |
 |
2 |
| 五 |
 |
1 |
(本小题满分12分)已知函数 ,
, 的最大值是1,最小正周期是
的最大值是1,最小正周期是 ,其图像经过点
,其图像经过点 .
.
(1)求 的解析式;
的解析式;
(2)设 、
、 、
、 为△ABC的三个内角,且
为△ABC的三个内角,且 ,
, ,求
,求 的值.
的值.
(本小题满分12分)某学校900名学生在一次百米测试中,成绩全部介于 秒与
秒与 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组 , ,第五组
, ,第五组 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计本年级900名学生中,成绩属于第三组的人数;
(3)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽2个同学组成一个实验组,设其中男同学的数量为 ,求
,求 的分布列和期望.
的分布列和期望.
(本小题满分14分)如图,斜三棱柱 中,侧面
中,侧面
 底面ABC,底面ABC是边长为2的等边三角形,侧面
底面ABC,底面ABC是边长为2的等边三角形,侧面 是菱形,
是菱形, ,E、F分别是
,E、F分别是 、AB的中点.
、AB的中点.
求证:(Ⅰ) ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
如图,实线部分的月牙形公园是由圆 上的一段优弧和圆
上的一段优弧和圆 上的一段劣弧围成,圆
上的一段劣弧围成,圆 和圆
和圆 的半径都是
的半径都是 ,点
,点 在圆
在圆 上,现要在公园内建一块顶点都在圆
上,现要在公园内建一块顶点都在圆 上的多边形活动场地.
上的多边形活动场地.

(Ⅰ)如图甲,要建的活动场地为△ ,求活动场地的最大面积;
,求活动场地的最大面积;
(Ⅱ)如图乙,要建的活动场地为等腰梯形 ,求活动场地的最大面积;
,求活动场地的最大面积;
如图1, 是直角△
是直角△ 斜边上的高,沿
斜边上的高,沿 把△
把△ 的两部分折成直二面角(如图2),
的两部分折成直二面角(如图2), 于
于 .
.
(Ⅰ)证明: ;
;
(Ⅱ)设 ,
, 与平面
与平面 所成的角为
所成的角为 ,二面角
,二面角 的大小为
的大小为 ,试用
,试用 表示
表示 ;
;
(Ⅲ)设 ,
, 为
为 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ? 若存在,求
? 若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
一个袋子中装有6个红球和4个白球,假设袋子中的每一个球被摸到可能性是相等的。
(Ⅰ)从袋子中任意摸出3个球,求摸出的球均为白球的概率;
(Ⅱ)一次从袋子中任意摸出3个球,若其中红球的个数多于白球的个数,则称“摸球成功”(每次操作完成后将球放回),某人连续摸了3次,记“摸球成功”的次数为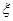 ,求
,求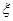 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
已知一家公司生产某种品牌服装的年固定成本为 万元,每生产
万元,每生产 千件需另投入
千件需另投入 万元.设该公司一年内生产该品牌服装
万元.设该公司一年内生产该品牌服装 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且
(Ⅰ)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大年利润.(注:年利润=年销售收入-年总成本).
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问3分,(Ⅲ)小问4分)
为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,记录了小李第 天打篮球的时间
天打篮球的时间 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率 的数据,其中
的数据,其中 .
.
算得: .
.
(Ⅰ)求投篮命中率 对打篮球时间
对打篮球时间 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)若小李明天准备打球 小时,预测他的投篮命中率.
小时,预测他的投篮命中率.
附:线性回归方程 中
中 ,其中
,其中 为样本平均数.
为样本平均数.
(本题共13分,第Ⅰ问6分,第Ⅱ问7分)
现有 道题,其中
道题,其中 道甲类题,
道甲类题, 道乙类题,张同学从中任取
道乙类题,张同学从中任取 道题解答.
道题解答.
(Ⅰ)求张同学至少取到 道乙类题的概率;
道乙类题的概率;
(Ⅱ)已知所取的 道题中有2道甲类题,
道题中有2道甲类题, 道乙类题.设张同学答对甲类题的概率都是
道乙类题.设张同学答对甲类题的概率都是 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用 表示张同学答对题的个数,求
表示张同学答对题的个数,求 的分布列和数学期望
的分布列和数学期望 .
.