高中数学解答题

(本小题满分14分）已知函数，其中
（1）写出的奇偶性与单调性（不要求证明）；
（2）若函数的定义域为，求满足不等式的实数的取值集合；
（3）当时，的值恒为负，求的取值范围.

（本小题满分12分）已知向量，函数f(x)=2的最小正周期为.(>0)
（1）求的递减区间；
（2）在中，分别是A、B、C的对边，若，，的面积为，求的值.

在中，为角所对的边，
（1）求角的大小；
（2）若，且，求的面积．

已知向量．
（1）当时，求的值；
（2）求在上的值域．

已知函数．
（1）求不等式的解集；
（2）设，若存在 ,使，求的取值范围。
（3）若对于任意的，关于的不等式在
区间上恒成立，求实数的取值范围．

已知函数
（1）写出的单调区间;
（2）设>0,求在上的最大值．

已知函数为奇函数。
（1）求的值；
（2）证明：函数在区间（1，）上是减函数；
（3）解关于x的不等式．

已知集合，不等式在集合上恒成立，求实数的取值范围.

已知函数＝ 
（1）判断函数的奇偶性，并说明理由；
（2）利用函数单调性定义证明函数在区间上为增函数.

不用计算器求下列各式的值.
（1）；  （2）设，求

(本小题14分)如图在四棱锥中，底面是矩形，平面，，点是中点，点是边上的任意一点.

（1）当点为边的中点时，判断与平面的位置关系，并加以证明；
（2）证明：无论点在边的何处，都有；
（3）求三棱锥的体积.

已知=是矩阵M=属于特征值λ₁=2的一个特征向量．
（Ⅰ）求矩阵M；
（Ⅱ）若，求M¹⁰a．

选修4﹣2：矩阵与变换
已知二阶矩阵M有特征值λ₁=4及属于特征值4的一个特征向量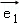=（），并有特征值λ₂=﹣1及属于特征值﹣1的一个特征向量=（），=（）．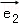
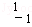（1）求矩阵M；
（2）求M⁵α．

给定矩阵，；求A⁴B．

已知矩阵M=的两个特征值分别为λ₁=﹣1和λ₂=4．
（1）求实数a，b的值；
（2）求直线x﹣2y﹣3=0在矩阵M所对应的线性变换作用下的象的方程．