(本小题14分)如图在四棱锥 中,底面
中,底面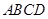 是矩形,
是矩形, 平面
平面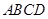 ,
,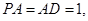
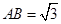 ,点
,点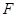 是
是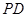 中点,点
中点,点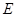 是
是 边上的任意一点.
边上的任意一点.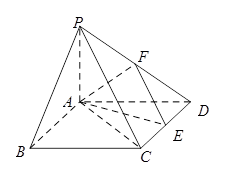
(1)当点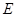 为
为 边的中点时,判断
边的中点时,判断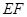 与平面
与平面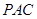 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)证明:无论点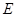 在
在 边的何处,都有
边的何处,都有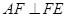 ;
;
(3)求三棱锥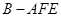 的体积.
的体积.
相关知识点
推荐套卷
(本小题14分)如图在四棱锥 中,底面
中,底面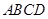 是矩形,
是矩形, 平面
平面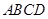 ,
,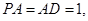
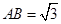 ,点
,点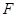 是
是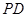 中点,点
中点,点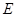 是
是 边上的任意一点.
边上的任意一点.
(1)当点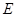 为
为 边的中点时,判断
边的中点时,判断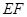 与平面
与平面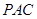 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)证明:无论点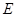 在
在 边的何处,都有
边的何处,都有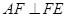 ;
;
(3)求三棱锥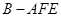 的体积.
的体积.