如图1,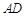 是直角△
是直角△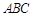 斜边上的高,沿
斜边上的高,沿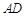 把△
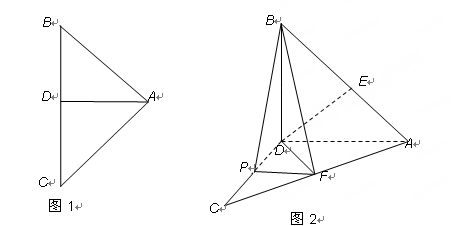
把△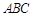 的两部分折成直二面角(如图2),
的两部分折成直二面角(如图2),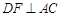 于
于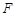 .
.
(Ⅰ)证明: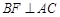 ;
;
(Ⅱ)设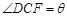 ,
,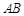 与平面
与平面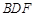 所成的角为
所成的角为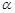 ,二面角
,二面角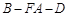 的大小为
的大小为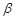 ,试用
,试用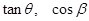 表示
表示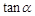 ;
;
(Ⅲ)设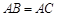 ,
,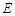 为
为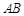 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使得
,使得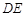 ∥平面
∥平面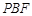 ? 若存在,求
? 若存在,求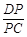 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关知识点
推荐套卷
如图1,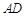 是直角△
是直角△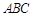 斜边上的高,沿
斜边上的高,沿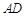 把△
把△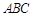 的两部分折成直二面角(如图2),
的两部分折成直二面角(如图2),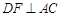 于
于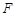 .
.
(Ⅰ)证明: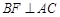 ;
;
(Ⅱ)设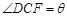 ,
,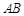 与平面
与平面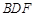 所成的角为
所成的角为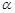 ,二面角
,二面角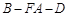 的大小为
的大小为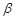 ,试用
,试用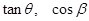 表示
表示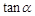 ;
;
(Ⅲ)设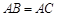 ,
,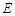 为
为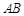 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使得
,使得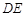 ∥平面
∥平面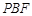 ? 若存在,求
? 若存在,求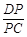 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.