(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分)一家公司计划生产某种小型产品的月固定成本为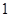 万元,每生产
万元,每生产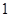 万件需要再投入
万件需要再投入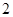 万元.设该公司一个月内生产该小型产品
万元.设该公司一个月内生产该小型产品 万件并全部销售完,每万件的销售收入为
万件并全部销售完,每万件的销售收入为 万元,且每万件国家给予补助
万元,且每万件国家给予补助 万元. (
万元. (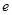 为自然对数的底数,
为自然对数的底数,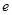 是一个常数.)
是一个常数.)
(Ⅰ)写出月利润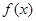 (万元)关于月产量
(万元)关于月产量 (万件)的函数解析式;
(万件)的函数解析式;
(Ⅱ)当月生产量在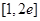 万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件). (注:月利润=月销售收入+月国家补助-月总成本).
万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件). (注:月利润=月销售收入+月国家补助-月总成本).
推荐套卷
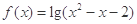 的定义域为集合
的定义域为集合 ,函数
,函数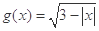 的定义域为集合
的定义域为集合 .
. ;
; ,且
,且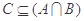 ,求实数
,求实数 的取值范围.
的取值范围.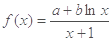 在点
在点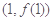 处的切线方程为
处的切线方程为 .
.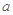 ,
, 的值;
的值;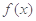 定义域内的任一个实数
定义域内的任一个实数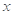 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 其中
其中 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.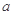 的值;
的值;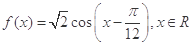 .
. 的值;
的值; ,求
,求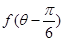 .
. .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间; 上的最大值与最小值的和为
上的最大值与最小值的和为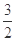 ,求
,求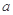 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号