（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问3分，（Ⅲ）小问4分）
为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，记录了小李第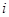
天打篮球的时间
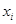（单位：小时）与当天投篮命中率
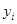的数据，其中
.
算得：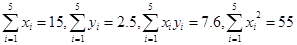
.
（Ⅰ）求投篮命中率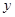
对打篮球时间
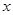的线性回归方程
；
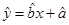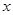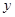（Ⅱ）判断变量与之间是正相关还是负相关；
（Ⅲ）若小李明天准备打球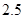
小时，预测他的投篮命中率.
附：线性回归方程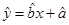中
，其中
为样本平均数.
与椭圆
的左焦点和右焦点的距离之比为
，求点
的焦点分别为
和
，长轴长为
，设直线
交椭圆
两点，求线段
的中点坐标。
轴上，离心率
，已知点
到这个椭圆上的点的最远距离是
，求这个椭圆的方程，并椭圆上到点
的距离等于
是椭圆
的两个焦点，
是椭圆上任意一点，求
的最大值和最小值。
是椭圆的一个焦点，
是短轴，
，求这个椭圆的离心率。推荐套卷
（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问3分，（Ⅲ）小问4分）
为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，记录了小李第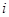天打篮球的时间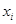（单位：小时）与当天投篮命中率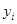的数据，其中.
算得：.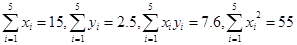
（Ⅰ）求投篮命中率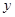对打篮球时间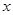的线性回归方程；
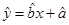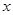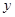（Ⅱ）判断变量与之间是正相关还是负相关；
（Ⅲ）若小李明天准备打球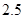小时，预测他的投篮命中率.
附：线性回归方程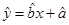中，其中为样本平均数.
粤公网安备 44130202000953号