高中数学解答题

在数列中，，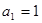
（1）求数列的通项；
（2）若存在，使得成立，求实数的最小值.

已知函数
（1）当时，求函数f（x）取得最大值和最小值时的值；
（2）设锐角△ABC的内角A、B、C的对应边分别是a，b，c，且a＝1，c∈N^*，若向量与向量平行，求c的值.

（本小题满分12分）我市某中学一研究性学习小组，在某一高速公路服务区，从小型汽车中按进服务区的先后，每间隔5辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段： ，，，，，，统计后得到如图的频率分布直方图．

（1）此研究性学习小组在采样中，用到的是什么抽样方法？并求这40辆小型汽车车速的众数和中位数的估计值．
（2）从车速在的车辆中任意抽取3辆车，求车速在，内都有车辆的概率．
（3）若从车速在的车辆中任意抽取3辆，求车速在的车辆数的数学期望．

（本小题满分12分）在如图所示的平面直角坐标系中，已知点和点，，且，其中为坐标原点．

（1）若，设点为线段上的动点，求的最小值;
（2）若，向量，，求的最小值及对应的值．

《选修4-5：不等式选讲》已知函数．
（1）证明：；
（2）求不等式的解集．

《选修4-4：坐标系与参数方程》已知直线L的参数方程： （t为参数）和圆C的极坐标方程： （θ为参数）．
（1）求圆C的直角坐标方程．
（2）判断直线L和圆C的位置关系．

已知．
（1）若，求曲线在点处的切线方程；
（2）若 求函数的单调区间．

已知椭圆C的中心在原点，焦点在轴上，左右焦点分别为，且，点（1，）在椭圆C上．
（1）求椭圆C的方程；
（2）过的直线与椭圆相交于两点，且的面积为，求直线的方程．

近几年出现各种食品问题，食品添加剂会引起血脂增高、血压增高、血糖增高等疾病．为了解三高疾病是否与性别有关，医院随机对入院的60人进行了问卷调查，得到了如下的列联表：

	患三高疾病	不患三高疾病	合计
男		6	30
女
合计	36

 
（1）请将如图的列联表补充完整；若用分层抽样的方法在患三高疾病的人群中抽人，其中女性抽多少人？
（2）为了研究三高疾病是否与性别有关，请计算出统计量，并说明你有多大的把握认为三高疾病与性别有关？        
下面的临界值表供参考：

	0．15	0．10	0．05	0．025	0．010	0．005	0．001
	2．072	2．706	3．841	5．024	6．635	7．879	10．828

 
（参考公式，其中）

如图五面体中，四边形为矩形，,四边形为梯形,
且,．

（1）求证：；   
（2）求此五面体的体积．

在中，角，,的对边分别是，，，其面积为，且．
（1）求; （2）若，,求．

《选修4-5：不等式选讲》已知函数．
（1）证明：；
（2）求不等式的解集．

《选修4-4：坐标系与参数方程》已知直线L的参数方程： （t为参数）和圆C的极坐标方程： （θ为参数）．
（1）求圆C的直角坐标方程．
（2）判断直线L和圆C的位置关系．

为迎接高一新生报到，学校向高三甲、乙、丙、丁四个实验班征召志愿者．统计如下：

班     级	甲	乙	丙	丁
志愿者人数	45	60	30	15

 
为了更进一步了解志愿者的来源，采用分层抽样的方法从上述四个班的志愿者中随机抽取50名参加问卷调查．
（1）从参加问卷调查的50名志愿者中随机抽取两名，求这两名来自同一个班级的概率；
（2）在参加问卷调查的50名志愿者中，从来自甲、丙两个班级的志愿者中随机抽取两名，用表示抽得甲班志愿者的人数，求的分布列和数学期望．

如图五面体中，四边形为矩形，,四边形为梯形,
且,．

（1）求证：；   
（2）求此五面体的体积．