(本小题满分13分)己知函数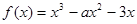
(1)若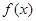 在区间
在区间 上是增函数,求实数
上是增函数,求实数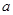 的取值范围;
的取值范围;
(2)若 是
是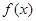 的极值点,求
的极值点,求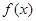 在
在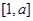 上的最大值;
上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数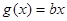 的图象与函数
的图象与函数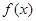 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由
(本小题满分13分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当 时,车流速度
时,车流速度 是车流密度
是车流密度 的一次函数.
的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:
辆/小时) 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
(本小题满分13分)已知数列 满足
满足 ,其中
,其中 N*.
N*.
(Ⅰ)设 ,求证:数列
,求证:数列 是等差数列,并求出
是等差数列,并求出 的通项公式
的通项公式 ;
;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 于
于 N*恒成立,若存在,求出
N*恒成立,若存在,求出 的最小值,若不存在,请说明
的最小值,若不存在,请说明
(本小题满分12分)如图,在底面为菱形的四棱锥 中,
中, ,
, 为
为 的中点,
的中点, ,
,

(1)求证: 平面
平面
(2)求 与面
与面 所成角的正弦值
所成角的正弦值
(本小题满分12分)已知二次函数 ,若
,若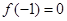 ,且对任意实数
,且对任意实数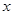 均有
均有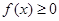 成立,设
成立,设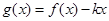
(1)当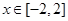 时,
时,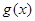 为单调函数,求实数
为单调函数,求实数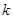 的范围
的范围
(2)当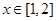 时,
时, 恒成立,求实数
恒成立,求实数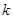 的范围.
的范围.
(本小题满分12分)已知向量 ,
, =
= ,函数
,函数 ,
,
(1)求函数f(x)的解析式及其单调递增区间;
(2)当x∈ 时,求函数f(x)的值域.
时,求函数f(x)的值域.
(本小题满分13分)设函数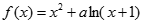 有两个极值点
有两个极值点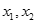 ,且
,且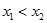 .
.
(1)求实数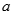 的取值范围;
的取值范围;
(2)讨论函数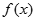 的单调性;
的单调性;
(3)若对任意的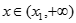 ,都有
,都有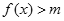 成立,求实数
成立,求实数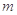 的取值范围.
的取值范围.
(本小题13分)为了保护环境,某工厂在政府部门的鼓励下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: ,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(Ⅰ)当 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?
(Ⅱ)当处理量为多少吨时,每吨的平均处理成本最少?
(本小题满分13分)直三棱柱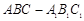 中,
中,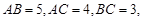
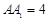 ,点
,点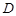 在
在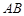 上.
上.
(Ⅰ)若 是
是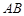 中点,求证:
中点,求证: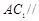 平面
平面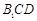 ;
;
(Ⅱ)当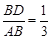 时,求二面角
时,求二面角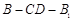 的余弦值.
的余弦值.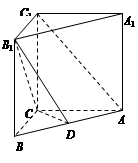
(本小题满分12分)已知数列 的前
的前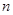 项和为
项和为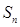 ,且有
,且有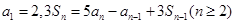 .
.
(1)求数列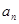 的通项公式;
的通项公式;
(2)若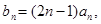 求数列
求数列 的前n项和
的前n项和
设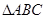 的内角
的内角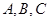 所对的边分别为
所对的边分别为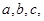 且
且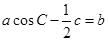 .
.
(1)求角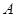 的大小;
的大小;
(2)若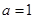 ,求
,求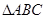 的周长的取值范围.
的周长的取值范围.
已知函数 ,
, (a为实数).
(a为实数).
(1)当a=5时,求函数 在
在 处的切线方程;
处的切线方程;
(2)求 在区间
在区间 上的最小值;
上的最小值;
(3)若存在两不等实数 ,使方程
,使方程 成立,求实数a的取值范围.
成立,求实数a的取值范围.
为改善购物环境,提高经济效益,某商场决定投资800万元改造商场内部环境,据调查,改造好购物环境后,任何一个月内(每月按30天计算)每天的顾客人数 与第x天近似地满足
与第x天近似地满足 (千人),且每位顾客人均购物金额数
(千人),且每位顾客人均购物金额数 近似地满足
近似地满足 (元).
(元).
(1)求该商场第x天的销售收入 (单位千元,1≤x≤30,
(单位千元,1≤x≤30, )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天纯收入的计量依据,商场决定以每日纯收入的5%收回投资成本,试问商场在两年内能否收回全部投资成本.
已知等差数列 的前n项和为
的前n项和为 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前n项和
的前n项和 .
.