湖南省衡阳市高三上学期五校联考文科数学试卷
命题“存在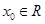 ,使得
,使得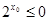 ”的否定是( )
”的否定是( )
A.不存在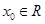 ,使得 ,使得 |
B.存在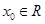 ,使得 ,使得 |
C.对任意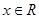 ,都有 ,都有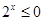 |
D.对任意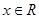 ,使得 ,使得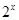 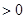 |
已知函数y=f(x)图象上每个点的纵坐标保持不变,将横坐标伸长到原来的2倍,然后将整个图象沿 轴向左平移
轴向左平移 个单位,得到的图象与y=
个单位,得到的图象与y= sin x的图象相同,则y=f(x)的函数表达式为( )
sin x的图象相同,则y=f(x)的函数表达式为( )
A. |
B. |
C. |
D. |
设向量 =
= ,
, =
= ,则“
,则“ ”是“
”是“ //
// ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos 2A=0,a=7,c=6,则b=( )
| A.10 | B.9 | C.8 | D.5 |
设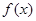 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若函数
上的两个函数,若函数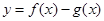 在
在 上有两个不同零点,则称
上有两个不同零点,则称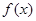 与
与 在
在 上是“关联函数”,区间
上是“关联函数”,区间 称为“关联区间”,若
称为“关联区间”,若 和
和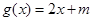 在
在 上是“关联函数”,则
上是“关联函数”,则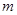 的范围为( )
的范围为( )
A. |
B.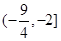 |
C. |
D.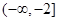 |
对于任意的两个实数对 和
和 规定
规定 当且仅当
当且仅当 ;
;
运算“ ”为:
”为: ,运算“
,运算“ ”为:
”为: ,设
,设 ,若
,若 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
(本小题满分12分)已知向量 ,
, =
= ,函数
,函数 ,
,
(1)求函数f(x)的解析式及其单调递增区间;
(2)当x∈ 时,求函数f(x)的值域.
时,求函数f(x)的值域.
(本小题满分12分)已知二次函数 ,若
,若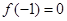 ,且对任意实数
,且对任意实数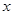 均有
均有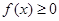 成立,设
成立,设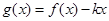
(1)当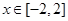 时,
时,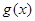 为单调函数,求实数
为单调函数,求实数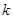 的范围
的范围
(2)当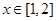 时,
时, 恒成立,求实数
恒成立,求实数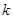 的范围.
的范围.
(本小题满分12分)如图,在底面为菱形的四棱锥 中,
中, ,
, 为
为 的中点,
的中点, ,
,

(1)求证: 平面
平面
(2)求 与面
与面 所成角的正弦值
所成角的正弦值
(本小题满分13分)已知数列 满足
满足 ,其中
,其中 N*.
N*.
(Ⅰ)设 ,求证:数列
,求证:数列 是等差数列,并求出
是等差数列,并求出 的通项公式
的通项公式 ;
;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 于
于 N*恒成立,若存在,求出
N*恒成立,若存在,求出 的最小值,若不存在,请说明
的最小值,若不存在,请说明
(本小题满分13分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当 时,车流速度
时,车流速度 是车流密度
是车流密度 的一次函数.
的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:
辆/小时) 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
 的定义域是( )
的定义域是( )



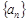 中,若
中,若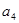 ,
,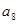 是方程
是方程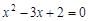 的两根,则
的两根,则 的值是 ( )
的值是 ( )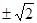

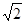
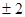
 ,
,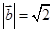 ,且
,且 ,则
,则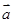 与
与 夹角的余弦值为( )
夹角的余弦值为( )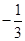
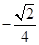

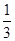
 (其中
(其中 ),若
),若 的图像如右图所示,则函数
的图像如右图所示,则函数 的图像大致为( )
的图像大致为( ) 




 ,满足
,满足 ,若
,若
 则
则
 的前n项和
的前n项和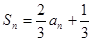 ,则{an}的通项公式是an=____ ____
,则{an}的通项公式是an=____ ____ 是偶函数,当
是偶函数,当 时,
时,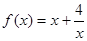 ,且当
,且当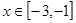 时,
时,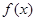 的值域是
的值域是 ,则
,则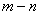 的值是
的值是  ,
, 为
为 中点,则
中点,则 、
、
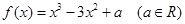
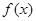 的图像在
的图像在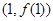 处的切线经过点
处的切线经过点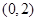 ,则
,则 =
= 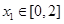 ,都存在
,都存在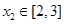 使得
使得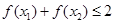 ,则实数
,则实数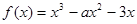
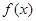 在区间
在区间 上是增函数,求实数
上是增函数,求实数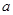 的取值范围;
的取值范围; 是
是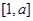 上的最大值;
上的最大值;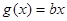 的图象与函数
的图象与函数 粤公网安备 44130202000953号
粤公网安备 44130202000953号