四川省成都实验外国语高三11月月考理科数学试卷
某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )
A. |
B. |
C. |
D. |
若(9x- )n(n∈N*)的展开式中第3项的二项式系数为36,则其展开式中的常数项为( )
)n(n∈N*)的展开式中第3项的二项式系数为36,则其展开式中的常数项为( )
| A.84 | B.-252 | C.252 | D.-84 |
在正方体ABCD-A'B'C'D'中,点P在线段AD'上运动,则异面直线CP与BA'所成的角θ的取值范围是 ( )
A. |
B. |
C. |
D. |
设函数 ,其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)-
,其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)- x-
x- 不同零点的个数为( )
不同零点的个数为( )
| A.2 | B.3 | C.4 | D.5 |
对于三次函数 ,给出定义:设
,给出定义:设 是函数
是函数 的导数,
的导数, 是
是 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数 ,则
,则 =( )
=( )
| A.2011 | B.2012 | C.2013 | D.2014 |
无重复数字的五位数a1a2a3a4a5, 当a1<a2, a2>a3, a3<a4, a4>a5时称为波形数,则由1,2,3,4,5任意组成的一个没有重复数字的五位数是波形数的概率为 .
若数列 满足:存在正整数
满足:存在正整数 ,对于任意正整数
,对于任意正整数 都有
都有 成立,则称数列
成立,则称数列 为周期数列,周期为
为周期数列,周期为 . 已知数列
. 已知数列 满足
满足 ,
, 现给出以下命题:
现给出以下命题:
①若 ,则
,则 可以取3个不同的值
可以取3个不同的值
②若 ,则数列
,则数列 是周期为
是周期为 的数列
的数列
③ 且
且 ,存在
,存在 ,
, 是周期为
是周期为 的数列
的数列
④ 且
且 ,数列
,数列 是周期数列.其中所有真命题的序号是 .
是周期数列.其中所有真命题的序号是 .
已知函数
(1)当 时,求函数f(x)取得最大值和最小值时
时,求函数f(x)取得最大值和最小值时 的值;
的值;
(2)设锐角△ABC的内角A、B、C的对应边分别是a,b,c,且a=1,c∈N*,若向量 与向量
与向量 平行,求c的值.
平行,求c的值.
某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3, ,10的十个小球.活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金.
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数 的方差是多少?
的方差是多少?
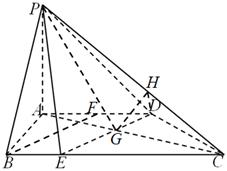
如图,在四棱锥 中,
中, //
// ,
, ,
, ,
, ,平面
,平面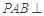 平面
平面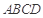 .
.
(1)求证:平面 平面
平面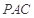 ;
;
(2)若直线 与平面
与平面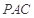 所成的角的正弦值为
所成的角的正弦值为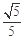 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值.
设椭圆E中心在原点,焦点在x轴上,短轴长为4,点Q(2, )在椭圆上.
)在椭圆上.
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且 ,求△OAB的面积的取值范围.
,求△OAB的面积的取值范围.
(3)过M( )的直线
)的直线 :
: 与过N(
与过N( )的直线
)的直线 :
: 的交点P(
的交点P( )在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求
)在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求 的值.
的值.
 ,N={x|y=
,N={x|y= },则
},则 =( )
=( )



 的前n项和为
的前n项和为 ,若
,若 为一确定常数,下列各式也为确定常数的是( )
为一确定常数,下列各式也为确定常数的是( )



 中,
中, ,
,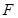 在线段
在线段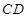 上,设
上,设 ,
, ,
, ,则
,则 的最小值为( )
的最小值为( )


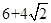
 ,其中
,其中 ,则
,则 ______.
______. 的位置关系为______________.
的位置关系为______________. 在不等式组
在不等式组 表示的平面区域内部及其边界上运动,则
表示的平面区域内部及其边界上运动,则 的取值范围是 .
的取值范围是 . 中,
中,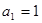 ,
,
 ;
; ,使得
,使得 成立,求实数
成立,求实数 的最小值.
的最小值. (
( 为自然对数的底数),
为自然对数的底数),

 ;
; 时,比较
时,比较 的大小,并说明理由;
的大小,并说明理由; (
( ).
). 粤公网安备 44130202000953号
粤公网安备 44130202000953号