设椭圆E中心在原点,焦点在x轴上,短轴长为4,点Q(2,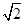 )在椭圆上.
)在椭圆上.
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且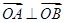 ,求△OAB的面积的取值范围.
,求△OAB的面积的取值范围.
(3)过M(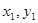 )的直线
)的直线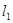 :
: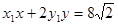 与过N(
与过N( )的直线
)的直线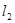 :
: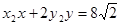 的交点P(
的交点P(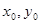 )在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求
)在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求 的值.
的值.
推荐套卷
设椭圆E中心在原点,焦点在x轴上,短轴长为4,点Q(2,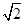 )在椭圆上.
)在椭圆上.
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且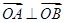 ,求△OAB的面积的取值范围.
,求△OAB的面积的取值范围.
(3)过M(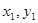 )的直线
)的直线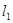 :
: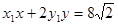 与过N(
与过N( )的直线
)的直线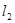 :
: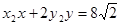 的交点P(
的交点P(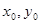 )在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求
)在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求 的值.
的值.