为了预防甲型H1N1流感,某学校对教室用药薰消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与t时间(小时)成正比,药物释放完毕后,y与t之间的函数关系式为 (a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(a为常数)如下图所示,根据图中提供的信息,回答下列问题.
(1)从药物释放开始,求每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始至少需要经过多少小时后,学生才可能回到教室.
相关知识点
推荐套卷
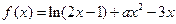 在
在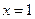 处取得极值.
处取得极值.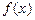 的单调区间;
的单调区间;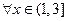 ,
,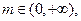
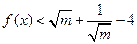 .
. 是
是 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角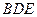 ?若存在,确定点N的位置;
?若存在,确定点N的位置;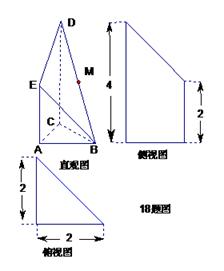
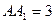 ,俯视图中
,俯视图中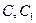 分别是所在边的中点,设
分别是所在边的中点,设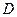 为
为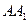 的中点.
的中点.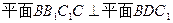 ;
;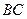 边上是否存在点
边上是否存在点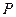 ,使
,使 ?若不存在,说明理由;若存在,请证明你的结论.
?若不存在,说明理由;若存在,请证明你的结论.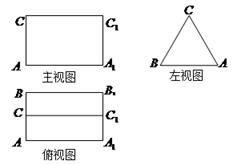
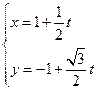 被圆
被圆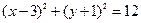 所截得的弦长。
所截得的弦长。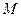 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到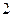 倍,纵坐标伸长到
倍,纵坐标伸长到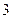 倍的伸压变换.求逆矩阵
倍的伸压变换.求逆矩阵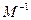 以及椭圆
以及椭圆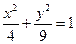 在
在 粤公网安备 44130202000953号
粤公网安备 44130202000953号