高中数学解答题

已知是上的奇函数，且当时，；
（1）求的解析式；
（2）作出函数的图象（不用列表），并指出它的增区间.

（本小题满分12分）已知函数，
（1）为何值时，有两个零点且均比－1大；
（2）求在上的最大值．

函数是定义在上的奇函数，且。
（1）求实数a，b，并确定函数的解析式；
（2）判断在（-1，1）上的单调性，并用定义证明你的结论；
（3）写出的单调减区间，并判断有无最大值或最小值？如有，写出最大值或最小值。（本小问不需要说明理由）

我国是水资源匮乏的国家为鼓励节约用水，某市打算出台一项水费政策措施，规定：每一季度每人用水量不超过5吨时，每吨水费收基本价1．3元；若超过5吨而不超过6吨时，超过部分水费加收200%；若超过6吨而不超过7吨时，超过部分的水费加收400%，如果某人本季度实际用水量为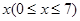吨，应交水费为。
（1）求、、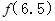的值；
（2）试求出函数的解析式。

已知，
（1）证明：
（2）计算的值

已知集合
（1）求；（2）求；（3）若，求a的取值范围。

已知点，圆，过点的动直线与圆交于两点，线段的中点为，O为坐标原点.
（1）求的轨迹方程；
（2）当时，求的方程及的面积.

已知圆M：（x＋1）²＋y²＝1，圆N：（x－1）²＋y²＝9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C.
（1）求C的方程；
（2）l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|.

设抛物线C：x²=2py（p>0）的焦点为F，准线为l，A为C上一点，已知以F为圆心，FA为半径的圆F交l于B，D两点.
（1）若∠BFD=90°,△ABD的面积为，求p的值及圆F的方程；
（2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值.

已知椭圆E的长轴的一个端点是抛物线的焦点，离心率是
（1）求椭圆E的方程；
（2）过点C（—1，0），斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使为常数？若存在，求出点M的坐标；若不存在，请说明理由。

已知圆C：和直线l：，点P是圆C上的一动点，直线与坐标轴的交点分别为点A、B，
（1）求与圆C相切且平行直线l的直线方程；
（2）求面积的最大值。

（本小题满分14分）已知定义在正实数集上的函数f（x）＝＋ax，g（x）＝4a²lnx＋b，其中a＞0，设两曲线y＝f（x）与y＝g（x）有公共点，且在公共点处的切线相同.
（1）若a＝1，求两曲线y＝f（x）与y＝g（x）在公共点处的切线方程；
（2）用a表示b，并求b的最大值.

（本小题满分13分）如图，点M（）在椭圆（a＞b＞0）上，且点M到两焦点的距离之和为4.

（1）求椭圆方程；
（2）设与MO（O为坐标原点）垂直的直线交椭圆于A、B（A、B不重合），求的取值范围.

（本小题满分12分）已知数列{a_n}满足a_n＝2a_n－1＋2ⁿ＋1（n∈N，n＞1），a₃＝27，数列{b_n}满足b_n＝（a_n＋t）.
（1）若数列{b_n}为等差数列，求b_n；
（2）在（1）的条件下，求数列{a_n}的前n项和S_n.

（本小题满分12分）甲、乙两家药厂生产同一型号药品，在某次质量检测中，两厂各有5份样品送检，检测的平均得分相等（检测满分为100分，得分高低反映该样品综合质量的高低）.成绩统计用茎叶图表示如下：

（1）求a；
（2）某医院计划采购一批该型号药品，从质量的稳定性角度考虑，你认为采购哪个药厂的产品比较合适？
（3）检测单位从甲厂送检的样品中任取两份作进一步分析，在抽取的两份样品中，求至少有一份得分在（90，100]之间的概率.